【题目】如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与OD交于点F,连接DF,DC.已知OA=OB,CA=CB,DE=10,DF=6.
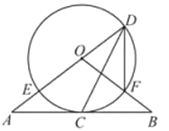
(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;
(2)求CD的长.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)①连接0C,易证OC⊥AB,即可判定直线AB是⊙O的切线;②根据等腰三角形的性质可得∠AOC=∠BOC,再由圆周角定理可得![]() ,所以∠FDC=∠EDC;(2)连接EF交OC于G,连接EC,先求得EF=8,根据垂径定理得EG=FG=4,再求得OG=3,GC=2,在Rt△EGC中,根据勾股定理可得CE=
,所以∠FDC=∠EDC;(2)连接EF交OC于G,连接EC,先求得EF=8,根据垂径定理得EG=FG=4,再求得OG=3,GC=2,在Rt△EGC中,根据勾股定理可得CE=![]() ,在Rt△ECD中,再由勾股定理可得CD=
,在Rt△ECD中,再由勾股定理可得CD=![]() .
.
试题解析:(1)证明:①连接0C,
∵OA=OB,AC=BC,∴OC⊥AB.
∴直线AB是⊙O的切线.
![]()
![]()
(2)连接EF交OC于G,连接EC.
∵DE是直径,∴∠DFE=∠DCE=90°
![]()
![]()
![]()
![]()
![]()
在Rt△EGC中,CE=![]()
在Rt△ECD中,CD=![]()

-
科目: 来源: 题型:
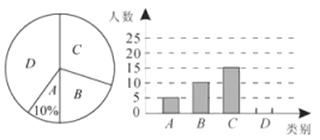
查看答案和解析>>【题目】襄阳市文化底蕴深厚,旅游资源丰富,古隆中、习家池、鹿门寺三个景区是人们节假日游玩的热点景区.张老师对八(1)班学生“五·一”小长假随父母到这三个景区游玩的计划做了全面调查,凋奄分四个类别:A 游三个景区;B 游两个景区;C 游一个景区;D 不到这三个景区游玩.现根据调查结果绘制了不完整饷条形统计图和扇形统计图,请结合图中信息解答下列问题.
(1)八(1)班共有学生 人,在扇形统计图中,表示“B 类别”的扇形的圆心角的度数为 ;
(2)请将条形统计图补充完整:
(3)若张华、李刚两名同学,各自从三个景区中随机选一个作为5月1日游玩的景区,则他们同时选中古隆中的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积为______;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(3)若连接AA′,BB′,则这两条线段之间的关系是______;
(4)在图中画出△ABC的高CD.

-
科目: 来源: 题型:
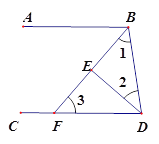
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F,∠1+∠2=90°.试问直线AB,CD在位置上有什么关系?∠2与∠3在数量上有什么关系?并证明你的猜想.
-
科目: 来源: 题型:
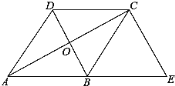
查看答案和解析>>【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)完成下面的推理说明:
已知:如图,
 ∥
∥ ,
, 、
、 分别平分
分别平分 和
和 .
.
求证:
 ∥
∥ .
.证明:
 、
、 分别平分
分别平分 和
和 (已知),
(已知), ,
, ( ).
( ). ∥
∥ ( ),
( ),  ( ).
( ). ( ).
( ).  (等式的性质).
(等式的性质). ∥
∥ ( ).
( ).(2)说出(1)的推理中运用了哪两个互逆的真命题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式,能用平方差公式计算的是( )
A.(-a+b)(b-a)
B.(2x+1)(-2x-1)
C.(-5y+3)(5y+3)
D.(-2m+n)(2m-n)
相关试题

