【题目】若抛物线y=ax2+bx+c如图所示,下列四个结论: ①abc<0;②b﹣2a<0;③a﹣b+c<0;④b2﹣4ac>0.
其中正确结论的个数是( )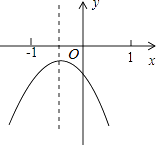
A.1
B.2
C.3
D.4
参考答案:
【答案】B
【解析】解:∵抛物线开口向下, ∴a<0,
∵抛物线的对称轴在y轴左侧,
∴b<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以①正确;
∵﹣1<﹣ ![]() <0,a<0,
<0,a<0,
∴2a<b,所以②错误;
∵x=﹣1时,y<0,
∴a﹣b+c<0,所以③正确;
∵抛物线与x轴没有交点,
∴b2﹣4ac<0,所以错误.
故选B.
用抛物线开口方向、抛物线的对称轴位置和抛物线与y轴的交点位置可判断a、b、c的符号,则可①进行判断;利用对称轴的位置得到﹣1<﹣ ![]() <0,a<0,然后根据不等式的性质可对②进行判断;利用自变量为﹣1时对应的函数值为负数可对③进行判断;根据抛物线与x轴的交点个数可对④进行判断.
<0,a<0,然后根据不等式的性质可对②进行判断;利用自变量为﹣1时对应的函数值为负数可对③进行判断;根据抛物线与x轴的交点个数可对④进行判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,二次函数y=﹣
 x2+
x2+  x+2的图象与x轴交于点A,B(点B在点A的左侧),与y轴交于点C.过动点H(0,m)作平行于x轴的直线l,直线l与二次函数y=﹣
x+2的图象与x轴交于点A,B(点B在点A的左侧),与y轴交于点C.过动点H(0,m)作平行于x轴的直线l,直线l与二次函数y=﹣  x2+
x2+  x+2的图象相交于点D,E.
x+2的图象相交于点D,E.
(1)写出点A,点B的坐标;
(2)若m>0,以DE为直径作⊙Q,当⊙Q与x轴相切时,求m的值;
(3)直线l上是否存在一点F,使得△ACF是等腰直角三角形?若存在,求m的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=120°,DE垂直平分AC交BC于D,垂足为E,若DE=2cm,则BC的长为( )
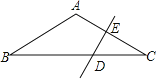
A. 6cm B. 8cm C. 10cm D. 12cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点M(
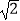 ,
, 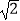 ),以点M为圆心,OM长为半径作⊙M.使⊙M与直线OM的另一交点为点B,与x轴,y轴的另一交点分别为点D,A(如图),连接AM.点P是
),以点M为圆心,OM长为半径作⊙M.使⊙M与直线OM的另一交点为点B,与x轴,y轴的另一交点分别为点D,A(如图),连接AM.点P是 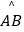 上的动点.
上的动点. 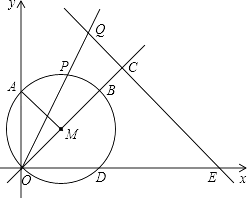
(1)写出∠AMB的度数;
(2)点Q在射线OP上,且OPOQ=20,过点Q作QC垂直于直线OM,垂足为C,直线QC交x轴于点E. ①当动点P与点B重合时,求点E的坐标;
②连接QD,设点Q的纵坐标为t,△QOD的面积为S.求S与t的函数关系式及S的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1),规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次交换,如此这样,连续经过2016次变换后,正方形ABCD的对角线交点M的坐标变为 .

-
科目: 来源: 题型:
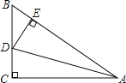
查看答案和解析>>【题目】如图,在
 ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB; ④BE+AC=AB.
ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB; ④BE+AC=AB.一定成立的结论有____________(填序号) .
-
科目: 来源: 题型:
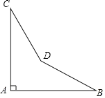
查看答案和解析>>【题目】某零件如图所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°,就断定这个零件不合格,你能说出其中的道理吗?
相关试题

