【题目】如图1,在 ![]() 中,
中, ![]() ,
, ![]() .点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为
.点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为 ![]() ,图1中某条线段的长为y,若表示y与x的函数关系的大致图象如图2所示,则这条线段可能是图1中的( )
,图1中某条线段的长为y,若表示y与x的函数关系的大致图象如图2所示,则这条线段可能是图1中的( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】C
【解析】当点D在AB上,则线段BD表示为y=x,线段AD表示为y=ABx为一次函数,不符合图象;
同理当点D在AC上,也为为一次函数,不符合图象;
如图,作OE⊥AB,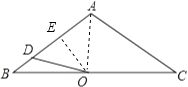
∵点O是BC中点,设AB=AC=a,∠BAC=120.
∴AO= ![]() ,BO=
,BO= ![]() ,OE=
,OE= ![]() ,BE=
,BE= ![]() ,
,
设BD=x,OD=y,AB=AC=a,
∴DE= ![]() x,
x,
在Rt△ODE中,
DE2+OE2=OD2 ,
∴y2=( ![]() x)2+(
x)2+( ![]() )2
)2
整理得:y2=x2 ![]() x+
x+ ![]() a2 ,
a2 ,
当0<xa时,y2=x2 ![]() x+
x+ ![]() a2 , 函数的图象呈抛物线并开口向上,
a2 , 函数的图象呈抛物线并开口向上,
由此得出这条线段可能是图1中的OD.
答案为:C
可逐项分析,分段分析,A、B答案对应的函数为一次函数,图像是直线型,D答案对应的OD长 应一直是减小的,与图像不符,因此C答案可分段分析,与图像最接近.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
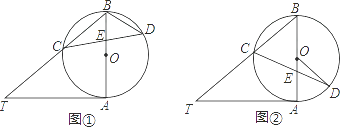
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC时,求∠CDO的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c中,自变量x与函数y之间的部分对应值如下表:

在该函数的图象上有A(x1 , y1)和B(x2 , y2)两点,且-1<x1<0,3<x2<4,y1与y2的大小关系正确的是( )
A.y1≥y2
B.y1>y2
C.y1≤y2
D.y1<y2 -
科目: 来源: 题型:
查看答案和解析>>【题目】关于
 的方程
的方程  的解是
的解是  =
=  ,
,  =
=  (
(  、
、  、
、  为常数,
为常数, 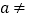 0),则方程
0),则方程  的解是 .
的解是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个角的两边与另一个角的两边分别平行,那么这两个角的大小有什么数量关系?请说明理由。(要求:画出图形,并写出已知,求证,证明过程)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC, EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75)

相关试题

