【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.

参考答案:
【答案】(1)B的坐标为(![]() ,4);(2)证明见解析;(3)1.
,4);(2)证明见解析;(3)1.
【解析】
试题分析:(1)由在△ABO中,∠OAB=90°,∠AOB=30°,OB=8,根据三角函数的知识,即可求得AB与OA的长,即可求得点B的坐标;
(2)首先可得CE∥AB,D是OB的中点,根据直角三角形斜边的中线等于斜边的一半,可证得BD=AD,∠ADB=60°,又由△OBC是等边三角形,可得∠ADB=∠OBC,根据内错角相等,两直线平行,可证得BC∥AE,继而可得四边形ABCD是平行四边形;
(3)首先设OG的长为x,由折叠的性质可得:AG=CG=8﹣x,然后根据勾股定理即可求得OG的长.
试题解析:(1)解:在△OAB中,∠OAB=90°,∠AOB=30°,OB=8,∴OA=OBcos30°=![]() =
=![]() ,AB=OBsin30°=8×
,AB=OBsin30°=8×![]() =4,∴点B的坐标为(
=4,∴点B的坐标为(![]() ,4);
,4);
(2)证明:∵∠OAB=90°,∴AB⊥x轴,∵y轴⊥x轴,∴AB∥y轴,即AB∥CE,∵∠AOB=30°,∴∠OBA=60°,∵DB=DO=4,∴DB=AB=4,∴∠BDA=∠BAD=120°÷2=60°,∴∠ADB=60°,∵△OBC是等边三角形,∴∠OBC=60°,∴∠ADB=∠OBC,即AD∥BC,∴四边形ABCE是平行四边形;
(3)解:设OG的长为x,∵OC=OB=8,∴CG=8﹣x,由折叠的性质可得:AG=CG=8﹣x,在Rt△AOG中,![]() ,即
,即![]() ,解得:x=1,即OG=1.
,解得:x=1,即OG=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若实数a,b满足a+b=0,则下列说法正确的是( )
A. a,b互为倒数 B. a,b异号
C. a的绝对值等于b D. a,b互为相反数
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x﹣4)2﹣5的顶点坐标和开口方向分别是( )
A. (4,﹣5),开口向上B. (4,﹣5),开口向下
C. (﹣4,﹣5),开口向上D. (﹣4,﹣5),开口向下
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当
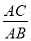 = 时,四边形ADFE是平行四边形.
= 时,四边形ADFE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.以轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由.(参考数据:
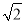 ≈1.4,
≈1.4,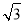 ≈1.7)
≈1.7)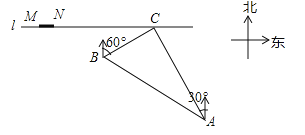
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
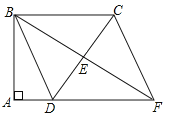
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(组),并把解集在数轴上表示.
(1)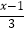 ﹣
﹣ 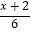 <
<  ﹣2
﹣2
(2)3≤ <6.
<6.
相关试题

