【题目】解不等式(组),并把解集在数轴上表示.
(1)![]() ﹣
﹣ ![]() <
< ![]() ﹣2
﹣2![]()
(2)3≤ ![]() <6.
<6.
参考答案:
【答案】
(1)解:去分母得,2(x﹣1)﹣(x+2)<3x﹣12,
去括号得,2x﹣2﹣x﹣2<3x﹣12,
移项得,2x﹣x﹣3x<2+2﹣12,
合并同类项得,﹣2x<﹣8,
把x的系数化为1得,x>4.
并在数轴上表示为:
![]()
(2)解:化为  ,
,
由①得,x≤﹣ ![]() ,
,
由②得,x>﹣ ![]() ,
,
故不等式组的解集为:﹣ ![]() <x≤﹣
<x≤﹣ ![]() ,
,
在数轴上表示为:
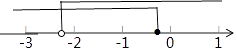
【解析】(1)去分母注意各项都需要乘6,移项要变号和除以负数时要变改变不等号;(2)在数轴上表示注意端点是实心还是圆圈.
【考点精析】解答此题的关键在于理解不等式的解集在数轴上的表示的相关知识,掌握不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈,以及对一元一次不等式的解法的理解,了解步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.以轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由.(参考数据:
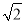 ≈1.4,
≈1.4,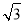 ≈1.7)
≈1.7)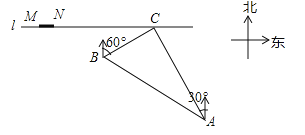
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
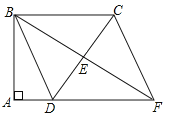
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在边AC、BC边上,且AD=CE,连接DE、DF、EF.

(1)求证:△ADF≌△CEF;
(2)试判断△DFE的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+2x+m的图象过点A(3,0).
(1)求m的值;
(2)当x取何值时,函数值y随x的增大而增大. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,属于必然事件的是( )
A.掷一枚硬币,正面朝下
B.三角形两边之和大于第三边
C.一个三角形三个内角的和小于180°
D.在一个没有红球的盒子里,摸到红球
相关试题

