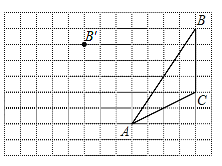
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为 1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B 的对应点 B′.
(1)在给定方格纸中画出平移后的△A′B′C′;
(2)线段 AA′与线段 BB′的数量和位置关系是___________;
(3)求△A′B′C′的面积.
参考答案:
【答案】(1)略;(2)平行且相等;(3)8
【解析】
(1)直接利用平移的性质得出各对应点位置进而得出答案;
(2)利用平移的性质得出对应点连线的关系;
(3)利用三角形面积求法得出答案.
(1)如图所示:△A′B′C′即为所求;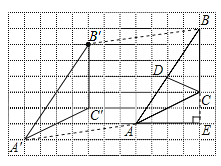
(2)线段AA′与线段BB′的关系是:平行且相等;故答案为:平行且相等;
(3)△A′B′C′的面积与△ABC的面积相等为:![]() ×4×4=8.
×4×4=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校准备组织七年级学生参加夏令营,已知:用3辆小客车和1辆大客车每次可运送学生105人;用一辆小客车和2辆大客车每次可运送学生110人,现有学生400人,计划租用小客车a辆,大客车b辆,一次送完,且恰好每辆车都坐满.
(1)1辆小客车和1辆大客车都坐满后一次可送多少名学生?
(2)请你帮学校设计出所有的租车方案;
(3)若小客车每辆需租金200元,大客车每辆需租金380元,请选出最省钱的方案,并求出最省租金.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,且AB=5,AC=6,过点D作AC的平行线交BC的延长线于点E,则△BDE的面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一等腰直角三角形纸片,以它的对称轴为折痕,将三角形对折,得到的三角形还是等腰直角三角形(如图).依照上述方法将原等腰直角三角形折叠四次,所得小等腰直角三角形的周长是原等腰直角三角形周长的倍.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学在
 ,
, 两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是
两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是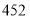 元,且随身听的单价比书包的单价的
元,且随身听的单价比书包的单价的 倍少
倍少 元.
元.(1)求该同学看中的随身听和书包的单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,超市
 所有商品打八五折销售,超市
所有商品打八五折销售,超市 全场购物每满
全场购物每满 元返购物券
元返购物券 元销售(不足
元销售(不足 元不返券,购物券全场通用),但他只带了
元不返券,购物券全场通用),但他只带了 元钱,如果他只在一家超市购买看中的这两样商品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
元钱,如果他只在一家超市购买看中的这两样商品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】小强与小刚都住在安康小区,在同一所学校读书.某天早上,小强
 从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留
从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留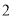 分钟,校车行驶途中始终保持匀速.当天早上,小刚
分钟,校车行驶途中始终保持匀速.当天早上,小刚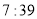 从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早
从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早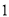 分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程
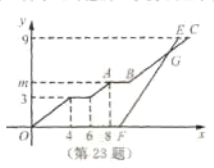
分钟到学校站点.他们乘坐的车辆从安康小区站出发所行驶路程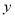 (千米)与行驶时间
(千米)与行驶时间 (分钟)之间的函数图象如图所示.
(分钟)之间的函数图象如图所示.(1)求点
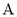 的纵坐标
的纵坐标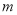 的值;
的值;(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在公路上行驶,其所走的路程和所用的时间可用下表表示:
时间t(min)
1
2.5
5
10
20
50
…
路程s(km)
2
5
10
20
40
100
…
(1)在这个变化过程中,自变量、因变量各是什么?
(2)当汽车行驶的路程为20 km时,所花的时间是多少分钟?
(3)随着t逐渐变大,s的变化趋势是什么?
(4)路程s与时间t之间的函数表达式为______________.
(5)按照这一行驶规律,当所花的时间t是300 min时,汽车行驶的路程s是多少千米?
相关试题

