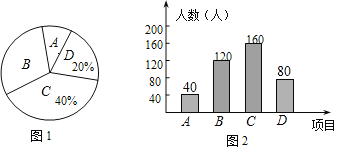
【题目】我市中小学全面开展“阳光体育”活动,某校在大课间中开设了A(体操)、B(乒乓球)、C(毽球)、D(跳绳)四项活动.为了解学生最喜欢哪一项活动,随机抽了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:

(1)这次被调查的学生共有 人;
(2)请将统计图2补充完整;
(3)统计图1中B项目对应的扇形的圆心角是 度;
(4)已知该校共有学生2500人,根据调查结果估计该校喜欢体操的学生有 人.
参考答案:
【答案】(1)400;(2)见解析;(3)108;(4)250.
【解析】
(1)由C项目的人数及其百分比可得答案;
(2)先根据D项目百分比及总人数求得D项目人数,再依据各项目人数之和等于总人数得出A项目的人数,即可补全图形;
(3)用360度乘以样本中B项目人数占总人数的比例即可得;
(4)用总人数乘以样本中A项目人数所占比例即可.
(1)这次被调查的学生共有160÷40%=400(人),
故答案为:400;
(2)D项目的人数为400×20%=80(人),
则A项目的人数为400-(120+160+80)=40(人),
补全图形如下:
(3)统计图1中B项目对应的扇形的圆心角是![]() ,
,
故答案为:108;
(4)根据调查结果估计该校喜欢体操的学生有![]() (人),
(人),
故答案为:250.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣x+5的图象与反比例函数
 (k≠0)在第一象限的图象交于A(1,n)和B两点.
(k≠0)在第一象限的图象交于A(1,n)和B两点.
(1)求反比例函数的解析式及点B坐标;
(2)在第一象限内,当一次函数y=-x+5的值大于反比例函数
 (k≠0)的值时,写出自变量x的取值范围.
(k≠0)的值时,写出自变量x的取值范围. -
科目: 来源: 题型:
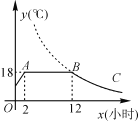
查看答案和解析>>【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=
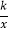 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:(1)恒温系统在这天保持大棚内温度18 ℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 是
是 内角
内角 的平分线,
的平分线, 是
是 外角
外角 的平分线,
的平分线, 是
是 外角
外角 的平分线,以下结论不正确的是( )
的平分线,以下结论不正确的是( )
A.
 B.
B.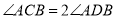
C.
 D.
D. 平分
平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.

∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2=___(___),
∴AB∥EF(___)
∵∠3=___(___)
又∠B=∠3(已知)
∴∠B=___(等量代换)
∴DE∥BC(___)
∴∠C=∠AED(___).
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形。
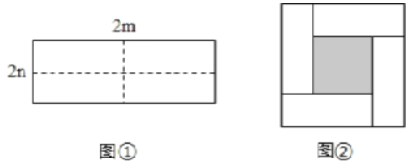
(1)用两种不同的方法表示图②中小正方形(阴影部分)的面积:
方法一:
 ;
;方法二:
 .
.(2)(m+n)
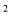 ,(mn)
,(mn) 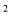 ,mn这三个代数式之间的等量关系为___
,mn这三个代数式之间的等量关系为___(3)应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求xy的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司经销甲种型号电脑,受疫情影响,电脑价格不断下降,今年四月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的甲种电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年四月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再进销售价为6000元的乙种型号电脑,四月份甲、乙两种电脑共销售15台,如果销售额不低于8万元,则乙种型号电脑销售不低于多少台?
相关试题

