【题目】如图，已知：点O是∠EPF的平分线上的一点，以点O为圆心的圆与角的两边分别交于点A、B和C、D。

（1）求证： =；

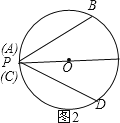
（2）若角的顶点P在圆内，上述结论还成立吗？若不成立，请说明理由；若成立，请加以证明。

参考答案：

【答案】（1）证明见解析

（2）上述结论还成立

【解析】试题分析：（1）如图1，作辅助线；由角平分线的性质得到OM=ON；由垂径定理得到AB=CD，即可解决问题．
（2）如图3，作辅助线；类似（1）中的证明方法，由角平分线的性质得到OM=ON；由垂径定理得到AB=CD，即可解决问题

试题解析：（1）：（1）如图1，过点O作OM⊥AB，ON⊥CD；


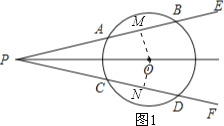
∵PO平分∠EPF，
∴OM=ON，
∴AB=CD

∴

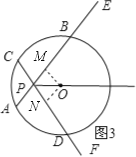
(2)如图2或图3，点P分别在⊙O上或⊙O内，（1）中的结论仍然成立；仅以图3为例证明如下：

如图3，过点O作OM⊥AB、ON⊥CD；

∵PO平分∠EPF，

∴OM=ON，

∴AB=CD

∴

关闭