【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系.
小明发现,利用轴对称做一个变化,在BC上截取CA′=CA,连接DA′,得到一对全等的三角形,从而将问题解决(如图2).
(1)求证:△ADC≌△A′DC;
(2)试猜想写出BC和AC、AD之间的数量关系,并给出证明.

参考答案:
【答案】(1)、答案见解析;(2)、BC=AC+AD;理由见解析
【解析】
试题分析:(1)、根据角平分线得出∠ACD=∠A′CD,然后得出△ADC和△A′DC全等,从而得出答案;(2)、根据全等得出DA′=DA,∠CA′D=∠A=60°,CA′=CA,然后根据等腰三角形的性质得出答案.
试题解析:(1)、∵CD平分∠ACB, ∴∠ACD=∠A′CD,
在△ADC和△A′DC中,  , ∴△ADC≌△A′DC(SAS)
, ∴△ADC≌△A′DC(SAS)
(2)、BC=AC+AD;
理由如下:由(1)得:△ADC≌△A′DC, ∴DA′=DA, ∠CA′D=∠A=60°, CA′=CA
∵∠ACB=90°, ∴∠B=90°﹣∠A=30°, ∵∠CA′D=∠B+∠BDA′,∴∠BDA′=30°=∠B,
∴DA′=BA′, ∴BA′=AD, ∴BC=CA′+BA′=AC+AD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
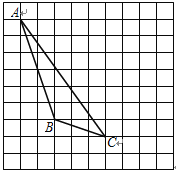
(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: _____________.
(3)画出△ABC的AB边上的高CD;垂足是D;
(4)图中△ABC的面积是_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点
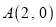 ,
, 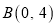 以
以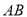 为斜边作一个等腰直角三角形
为斜边作一个等腰直角三角形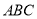 ,则点
,则点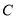 的坐标为______.
的坐标为______.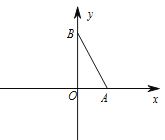
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某市初三学生的体育测试成绩和课外体育锻炼时间的情况,现从全市初三学生体育测试成绩中随机抽取120名学生的体育测试成绩作为样本.体育成绩分为四个等次:优秀、良好、及格、不及格.
(1)试求样本扇形图中体育成绩“良好”所对扇形圆心角的度数;
(2)统计样本中体育成绩“优秀”和“良好”学生课外体育锻炼时间表(如图表所示),请将图表填写完整(记学生课外体育锻炼时间为
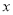 小时);
小时);(3)全市初三学生中有14400人的体育测试成绩为“优秀”和“良好”,请估计这些学生中课外体育锻炼时间不少于4小时的学生人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把半径为4cm的半圆围成一个圆锥,则圆锥的底面圆半径为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. x4x4=x16 B. (a3)2a4=a9
C. (ab2)3÷(﹣ab)2=﹣ab4 D. (a6)2÷(a4)3=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2b-2c)2等于_______;
相关试题

