【题目】如图、直角梯形![]() 中、
中、![]() 、
、![]() 、
、![]() 于
于![]() 、连接
、连接![]() ,
,![]() 垂直
垂直![]() 交
交![]() 于
于![]() .
.
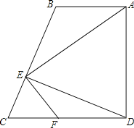
![]() 求证:
求证:![]() ;
;
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() .
.![]() ,则
,则![]() ________.
________.
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】
(1)根据条件可以得出∠EFC=∠EAD,∠CEF=∠AED,进而可以证明△AED∽△FEC.
(2)根据条件可以证明A、D、F、B、A四点共圆,由∠BEA=∠FED,推出结论.
(3)设AB=a,CD=b,通过辅助线,利用方程的思想解决问题.
解:![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]()
∴![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]() .
.
![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴四边形![]() 四点共圆,
四点共圆,
∵![]() ,
,
∴四边形![]() 四点共圆,
四点共圆,
∴![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五点共圆,
五点共圆,
∵![]() ,
,
∴![]() .
.
![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,过点
,过点![]() 作
作![]() 垂足为
垂足为![]() 交
交![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() .
.

∵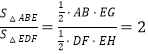 ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,设
,设![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
∵![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∵![]()
∴四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]()
∴![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ①
①
∵![]() ,
,
∴![]() ②
②
由①②消去![]() 得
得![]()
∴![]() ,(或
,(或![]() 舍弃)
舍弃)
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
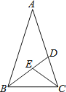
查看答案和解析>>【题目】如图,等腰
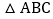 中,腰
中,腰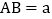 ,
,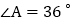 ,
,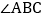 的平分线交
的平分线交 于
于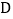 ,
,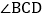 的平分线交
的平分线交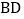 于
于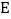 .设
.设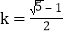 ,则
,则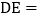 ( )
( )
A. k2a B. k3a C.
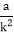 D.
D. 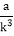
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊿
 中,
中, ,点
,点 分别在
分别在 边上,且
边上,且 ,
,  .
.⑴.求证:⊿
 是等腰三角形;
是等腰三角形;⑵.当
 时,求
时,求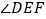 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解决下列两个问题:
(1)如图(1),在
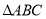 中,
中,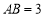 ,
,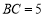 ,
,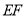 垂直平分
垂直平分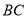 ,点
,点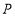 在直线
在直线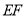 上,直接写出
上,直接写出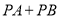 的最小值,并在图中标出当
的最小值,并在图中标出当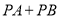 取最小值时点
取最小值时点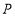 的位置;
的位置;(2)如图(2),点
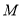 ,
,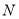 在
在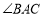 的内部,请在
的内部,请在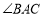 的内部求作一点
的内部求作一点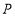 ,使得点
,使得点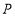 到
到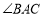 两边的距离相等,且使
两边的距离相等,且使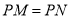 .(尺规作图,保留作图痕迹,无需证明).
.(尺规作图,保留作图痕迹,无需证明).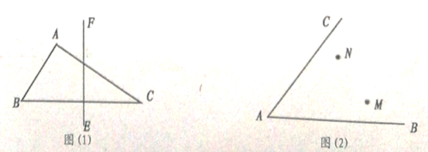
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.

(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片ABCD沿对角线AC折叠,设点D落在D′处,BC交AD′于点E,AB=6cm,BC=8cm,求阴影部分的面积.
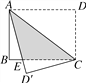
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:

(1)乙队开挖到30m时,用了_____ h. 开挖6h时甲队比乙队多挖了____ m;
(2)请你求出:
①甲队在
 的时段内,y与x之间的函数关系式;
的时段内,y与x之间的函数关系式;②乙队在
 的时段内,y与x之间的函数关系式;
的时段内,y与x之间的函数关系式;(3)当x 为何值时,甲、 乙两队在 施工过程中所挖河渠的长度相等?
相关试题

