【题目】如图①,在长方形![]() 中,
中,![]() 。点
。点![]() 从
从![]() 出发,沿
出发,沿![]() 路线运动,到
路线运动,到![]() 停止;点
停止;点![]() 出发时的速度为每秒
出发时的速度为每秒![]() ,7秒时点
,7秒时点![]() 的速度变为每秒
的速度变为每秒![]() ,图②是点
,图②是点![]() 出发
出发![]() 秒后,
秒后,![]() 的面积
的面积![]() 与
与![]() (秒)的关系图象;
(秒)的关系图象;

(1)根据题目提供的信息,求出![]() 的值为______________、
的值为______________、![]() 的值为_________
的值为_________![]() 的值为___________;
的值为___________;
(2)设点![]() 离开点
离开点![]() 的路程为
的路程为![]() ,
,
①7.5秒时,![]() 的值为_____________________;
的值为_____________________;
②请求出当动点![]() 改变速度后,
改变速度后,![]() 与
与![]() 的关系式;
的关系式;
(3)点![]() 出发后几秒,
出发后几秒,![]() 的面积
的面积![]() 是长方形
是长方形![]() 面积的
面积的![]() ?并说明理由。
?并说明理由。
参考答案:
【答案】(1)![]() 的值为28,
的值为28,![]() 的值为3,
的值为3,![]() 的值为14;(2)①8.5 ; ②
的值为14;(2)①8.5 ; ② ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据三角形的面积公式可求a、b及图②中c的值;
(2)①根据“速度变化前的路程+速度变化后的路程”求解即可;
②确定y与x的等量关系后列出关系式即可;
(3)①P在AB上运动时,S△APD=![]() AD×AP,AP为运动时间t的一次函数;
AD×AP,AP为运动时间t的一次函数;
②P在BC上运动时S△APD=![]() AD×AB为定值.
AD×AB为定值.
③P在DC段上运动时,S△APD=![]() AD×DP.DP为P点运动时间的一次函数.
AD×DP.DP为P点运动时间的一次函数.
先计算△APD的面积,然后将计算出来的数值代入所求函数的不同分段,解出对应的x的值,若解出的x值在对应的分段区间内,则x的值即为所求的解,反之则不是.
(1)根据图象可知S△APD=![]() AD×AP=
AD×AP=![]() ×8×(1×7)=28
×8×(1×7)=28
∴a=28;
∵AP=7,也就是P在AB上移动到了7cm,所剩部分为3cm,
当x=8时,S为40,且面积不发生变化,即P点到B点用了1秒,距离是3cm.
∴b=3cm/s,
c=18÷3+7+1=14s
(2)①∵7.5>7
∴y的值为:7×1+(7.5-7)×3=8.5cm;
②分三部分:i)运动时间从7秒到8时,
∵a=28,b=3,
∴设动点P改变速度后y与出发后的运动时间x(秒)的函数关系式为:y=kx+b,
把(7,28),(8,40)分别代入解析式得,
![]() ,
,
解得,![]()
∴y与x之间的函数关系式为:y=12x-56;
ii)运动时间从8秒到10![]() 秒时,y=40,
秒时,y=40,
iii)运动时间从10![]() 秒到14秒时,设y与x(秒)的函数关系式为:y=mx+n,
秒到14秒时,设y与x(秒)的函数关系式为:y=mx+n,
把(10![]() ,40),(14,0)代入得,
,40),(14,0)代入得,

解得,![]()
∴y与x(秒)的函数关系式为:y=-12x+168,
∴y与x(秒)的函数关系式为 ;
;
(3)S△APD=![]() s四边形ABCD=
s四边形ABCD=![]() AD×AB=16,
AD×AB=16,
①当0≤x≤7时
AP=x(cm)
S△APD=![]() AD×AP=4x
AD×AP=4x
∴4x=16,
解得,x=4
②当7<x≤8时
AP=7+(x-7)×3=3x-14
S△APD=![]() AD×AP=
AD×AP=![]() x-7
x-7
∴![]() x-7=16
x-7=16
解得,x=![]() (不符合题意,舍去)
(不符合题意,舍去)
③当P从B点运动到C点时
S△APD=![]() AD×AB=40≠16;
AD×AB=40≠16;
④当10![]() <x≤14时
<x≤14时
S△APD=-12x+168=16,
解得,x=![]() .
.
所以点P出发后4秒或![]() 秒,△APD的面积S1是长方形ABCD面积的
秒,△APD的面积S1是长方形ABCD面积的![]() .
.
-
科目: 来源: 题型:
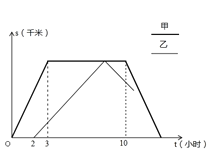
查看答案和解析>>【题目】甲乙两车从A市去往B市,甲比乙出发了2个小时,甲到达B市后停留一段时间返回,乙到达B市后立即返回.甲车往返的速度都为40千米/时,乙车往返的速度都为20千米/时,下图是两车距A市的路程S(千米)与行驶时间t(小时)之间的函数图象,请结合图象回答下列问题:
(1)A、B两市的距离是 千米,甲到B市后 小时乙到达B市;
(2)求甲车返回时的路程s(千米)与时间t(小时)之间的函数关系式,并写出自变量t的取值范围;
(3)请直接写出甲车从B市往回返后再经过几小时两车相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:如图,点
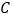 在
在 的一边
的一边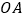 上,过点
上,过点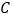 的直线
的直线 平行直线
平行直线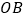 ,
, 平分
平分 ,
,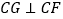 于点
于点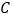 .
.(1)求证:
 平分
平分 ;
;(2)当
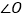 为多少度时,
为多少度时, 平分
平分 ,并说明理由。
,并说明理由。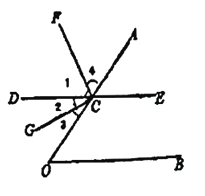
(1)证明:∵
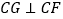 (已知)
(已知)∴
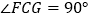 (垂直定义)
(垂直定义)即

又∵
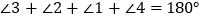 (平角定义)
(平角定义)∴
 ,
,∵
 平分
平分 ,
,∴
 (角平分线定义)
(角平分线定义)∴
 (_____________________)
(_____________________)即
 平分
平分 ;
;(2)解:
 时,
时,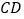 平分
平分 ,理由如下:
,理由如下:∵
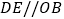 ,
,∴
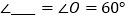 (____________________________),
(____________________________),∴
 _________________°
_________________°又∵
 平分
平分 ,
,∴
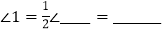 °,
°,∴
 (等量代换)
(等量代换)即
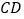 平分
平分 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表数据是科研小组在某地区根据调查获取的:“距离地面的高度(千米)与此处的温度(摄氏度)”的关系。
距离地面高度/千米
0
1
2
3
4
5
温度/摄氏度
20
14
8
2
-4
-10
根据上表,请你回答:
(1)上表中___________是自变量;_________________是因变量;
(2)如果用
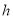 表示距离地面的高度(千米),
表示距离地面的高度(千米),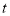 表示温度(摄氏度),请你写出
表示温度(摄氏度),请你写出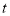 与
与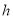 的关系式____________________________________;
的关系式____________________________________;(3)请你利用(2)的结论,求该地区:①距离地面6.2千米的高空温度是多少?②当高空某处温度为-52度时,该处的高度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在平面直角坐标系中,对于任意两点
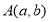 ,
,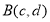 ,若点
,若点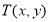 满足
满足 ,
,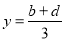 ,那么称点
,那么称点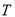 是点
是点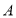 ,
,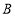 的融合点.
的融合点.例如:
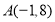 ,
,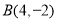 ,当点
,当点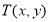 满是
满是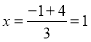 ,
, 时,则点
时,则点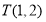 是点
是点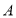 ,
,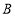 的融合点,
的融合点,
(1)已知点
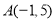 ,
,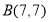 ,
,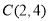 ,请说明其中一个点是另外两个点的融合点.
,请说明其中一个点是另外两个点的融合点.(2)如图,点
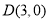 ,点
,点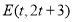 是直线
是直线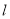 上任意一点,点
上任意一点,点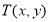 是点
是点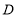 ,
,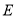 的融合点.
的融合点.①试确定
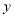 与
与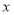 的关系式.
的关系式.②若直线
 交
交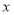 轴于点
轴于点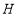 ,当
,当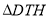 为直角三角形时,求点
为直角三角形时,求点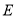 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】请在横线上填上合适的内容,完成下面的证明:
如图,射线AH交折线ACGFEN于点B、D、E.已知∠A=∠1,∠C=∠F,BM平分∠CBD,EN平分∠FEH.求证:∠2=∠3.

证明:∵∠A=∠1(已知)
∴AC∥GF( )
∴( )( )
∵∠C=∠F(已知)
∴∠F=∠G
∴( )( )
∴( )( )
∵BM平分∠CBD,EN平分∠FEH
∴∠2= ∠3=
∴∠2=∠3
相关试题

