【题目】已知正方形![]() 与正方形(点C、E、F、G按顺时针排列),是的中点,连接,.
与正方形(点C、E、F、G按顺时针排列),是的中点,连接,.
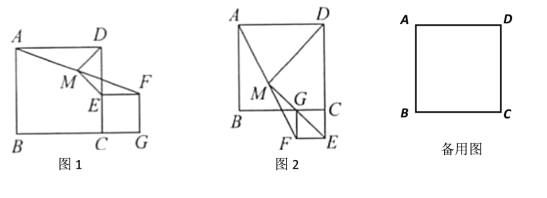
(1)如图1,点![]() 在上,点在的延长线上,
在上,点在的延长线上,
求证:![]() =ME,
=ME,![]() ⊥.ME
⊥.ME
简析: 由是的中点,AD∥EF,不妨延长EM交AD于点N,从而构造出一对全等的三角形,即 ≌ .由全等三角形性质,易证△DNE是 三角形,进而得出结论.
(2)如图2, 在![]() 的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.
的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.
(3)当AB=5,CE=3时,正方形的顶点C、E、F、G按顺时针排列.若点![]() 在直线CD上,则DM= ;若点E在直线BC上,则DM= .
在直线CD上,则DM= ;若点E在直线BC上,则DM= .
参考答案:
【答案】(1)等腰直角;(2)结论仍成立,见解析;(3)![]() 或
或![]() ,
,![]() .
.
【解析】
(1)结论:DM⊥EM,DM=EM.只要证明△AMH≌△FME,推出MH=ME,AH=EF=EC,推出DH=DE,因为∠EDH=90°,可得DM⊥EM,DM=ME;
(2)结论不变,证明方法类似;
(3)分两种情形画出图形,理由勾股定理以及等腰直角三角形的性质解决问题即可;
解:(1) △AMN ≌ △FME ,等腰直角.
如图1中,延长EM交AD于H.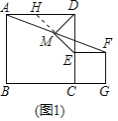
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴△AMH≌△FME,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴DM⊥EM,DM=ME.
(2)结论仍成立.
如图,延长EM交DA的延长线于点H,
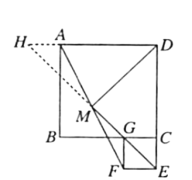
∵四边形ABCD与四边形CEFG都是正方形,
∴![]() ,
,![]() ,
,
∴AD∥EF,∴![]() .
.
∵![]() ,
,![]() ,
,
∴△AMF≌△FME(ASA), …
∴![]() ,
,![]() ,∴
,∴![]() .
.
在△DHE中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,DM⊥EM.
,DM⊥EM.
(3)①当E点在CD边上,如图1所示,由(1)的结论可得三角形DME为等腰直角三角形,则DM的长为![]() ,此时
,此时![]() ,所以
,所以![]() ;
;
②当E点在CD的延长线上时,如图2所示,由(2)的结论可得三角形DME为等腰直角三角形,则DM的长为![]() ,此时
,此时![]() ,所以
,所以![]() ;
;
③当E点在BC上是,如图三所示,同(1)、(2)理可得到三角形DME为等腰直角三角形,
证明如下:∵四边形ABCD与四边形CEFG都是正方形, 且点E在BC上
∴AB//EF,∴![]() ,
,
∵M为AF中点,∴AM=MF
∵在三角形AHM与三角形EFM中:
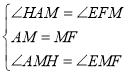 ,
,
∴△AMH≌△FME(ASA),
∴![]() ,
,![]() ,∴
,∴![]() .
.
∵在三角形AHD与三角形DCE中:
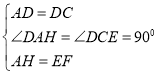 ,
,
∴△AHD≌△DCE(SAS),
∴![]() ,
,
∵∠ADC=∠ADH+∠HDC=90°,
∴∠HDE=∠CDE+∠HDC=90°,
∵在△DHE中,![]() ,
,![]() ,
,![]() ,
,
∴三角形DME为等腰直角三角形,则DM的长为![]() ,此时在直角三角形DCE中
,此时在直角三角形DCE中![]() ,所以
,所以![]()
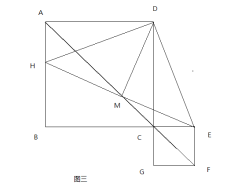
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据:
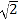 ≈1.4,
≈1.4, 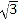 ≈1.7).
≈1.7).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班去商场为书法比赛买奖品,书包每个定价40元,文具盒每个定价8元,商场实行两种优惠方案:①买一个书包送一个文具盒:②按总价的9折付款.若该班需购买书包10个,购买文具盒若干个(不少于10个).
(1)当买文具盒40个时,分别计算两种方案应付的费用;
(2)当购买文具盒多少个时,两种方案所付的费用相同;
(3)如何根据购买文具盒的个数,选择哪种优惠方案的费用比较合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为6,点B是数轴上在A左侧的一点,且A,B两点间的距离为11,动点P从点A出发,以每秒3个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数是 ,当点P运动到AB中点时,它所表示的数是 ;
(2)动点Q从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,若P,Q两点同时出发,求点P与Q运动多少秒时重合?
(3)动点Q从点B出发,以每秒2个单拉长度的速度沿数轴向左匀速运动,若P,Q两点同时出发,求:
①当点P运动多少秒时,点P追上点Q?
②当点P与点Q之间的距离为8个单位长度时,求此时点P在数轴上所表示的数.
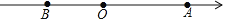
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,现有一张宽为12 cm的练习纸,相邻两条格线间的距离均为0.6 cm.调皮的小聪在纸的左上角用印章印出一个矩形卡通图案,图案的顶点恰好在四条格线上,已知sinα=
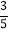 .
.(1)求一个矩形卡通图案的面积;
(2)若小聪在第一个图案的右边以同样的方式继续盖印,最多能印几个完整的图案?
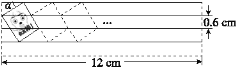
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,点E、M分别为直线AB、CD上的点,点N为两平行线间的点,连接NE、NM,过点N作NG平分∠ENM,交直线CD于点G,过点N作NF⊥NG,交直线CD于点F,若∠BEN=160°,则∠NGD﹣∠MNF=__度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若AB是⊙O内接正五边形的一边,AC是⊙O内接正六边形的一边,则∠BAC等于( )
A. 120° B. 6° C. 114° D. 114°或6°
相关试题

