【题目】春季是流感高发的季节,为此,某校为预防流感,对教室进行熏药消毒.在对教室进行消毒的过程中,先经过10min的药物燃烧,再封闭教室15min,然后打开门窗进行通风.已知室内空气中含药量![]() 与药物在空气中的持续时间
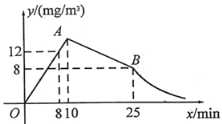
与药物在空气中的持续时间![]() 之间的函数关系式如图所示(即图中线段OA、线段AB和双曲线在点B及其右侧部分),请根据图中信息解答下列问题:
之间的函数关系式如图所示(即图中线段OA、线段AB和双曲线在点B及其右侧部分),请根据图中信息解答下列问题:
(1)求药物燃烧阶段和打开门窗进行通风阶段![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)若室内空气中的含药量不低于![]() 且持续时间不少于35min,才能有效消灭病毒,则此次消毒是否有效?请说明理由.
且持续时间不少于35min,才能有效消灭病毒,则此次消毒是否有效?请说明理由.
参考答案:
【答案】(1)药物燃烧阶段y1=![]() x,打开门窗进行通风阶段
x,打开门窗进行通风阶段![]() ,
,
(2)有效,理由见解析
【解析】
(1)依题意可知OA段是药物燃烧阶段,经过点(8,12),即可进行求解;打开门窗进行通风阶段为反比例函数,经过点B(25,8),故可求解;(2)求出AO段与反比例函数段含药量为![]() 的时间,计算出持续时间,即可进行判断.
的时间,计算出持续时间,即可进行判断.
(1)设药物燃烧阶段OA解析式:y1=k1x,∵经过点(8,12)
∴k1=![]() ,故y1=
,故y1=![]() x
x
设打开门窗进行通风阶段为![]() ,经过点B(25,8),故k2=200,
,经过点B(25,8),故k2=200,
∴![]() ,
,
(2)令y1=5,得x=![]() ,
,
令y2=5,得x=40,
∴室内空气中的含药量不低于![]() 的持续时间为40-
的持续时间为40-![]() =
=![]() >35,故此次消毒有效.
>35,故此次消毒有效.
-
科目: 来源: 题型:
查看答案和解析>>【题目】食品安全关乎民生,食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存.某饮料厂为了解A、B两种饮料添加剂的添加情况,随机抽检了A种30瓶,B种70瓶,检测发现,A种每瓶比B种每瓶少1克添加剂,两种共加入了添加剂270克,求A、B两种饮料每瓶各加入添加剂多少克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2
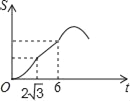
 为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
A.
 B.
B. 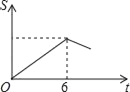 C.
C. 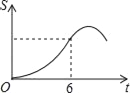 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校办公楼前有一长为m,宽为n的长方形空地,在中心位置留出一个直径为2b的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.

(1)用含字母和π的式子表示出阴影部分的面积S;
(2)当m=8,n=6,
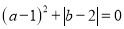 时,阴影部分的面积是多少?(π取3)
时,阴影部分的面积是多少?(π取3) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点G在正方形ABCD的对角线AC上,GE⊥BC,GF⊥CD,垂足分别为点E,F.
(1)求证:四边形CEGF是正方形;
(2)将正方形CEGF绕点C顺时针旋转
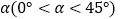 ,如图所示,线段BE与DF是否相等?为什么?
,如图所示,线段BE与DF是否相等?为什么?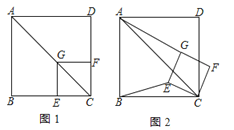
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,一次函数
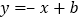 的图像与反比例函数
的图像与反比例函数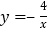 在第二象限内的图像相交于点A,与
在第二象限内的图像相交于点A,与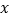 轴的负半轴交于点B,与
轴的负半轴交于点B,与 轴的负半轴交于点C.
轴的负半轴交于点C.(1)求∠BCO的度数;
(2)若
 轴上一点M的纵坐标是4,且B点坐标为(-3,0),求AM的长.
轴上一点M的纵坐标是4,且B点坐标为(-3,0),求AM的长.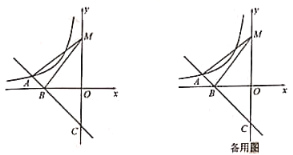
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

