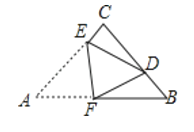
【题目】如图,在△ABC中, ![]() , AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则
, AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则![]() 的值为_____________.
的值为_____________.
【答案】![]()
【解析】分析:过点D作DG![]() AB于点G.根据折叠性质,可得AE=DE=2,AF=DF,CE=1,
AB于点G.根据折叠性质,可得AE=DE=2,AF=DF,CE=1,
在Rt△DCE中,由勾股定理求得![]() ,所以DB=
,所以DB=![]() ;在Rt△ABC中,由勾股定理得
;在Rt△ABC中,由勾股定理得![]() ;在Rt△DGB中,由锐角三角函数求得
;在Rt△DGB中,由锐角三角函数求得![]() ,
, ![]() ;
;
设AF=DF=x,则FG= ![]() ,在Rt△DFG中,根据勾股定理得方程
,在Rt△DFG中,根据勾股定理得方程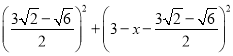 =
=![]() ,解得
,解得![]() ,从而求得
,从而求得![]() .的值
.的值
详解:
如图所示,过点D作DG![]() AB于点G.
AB于点G.
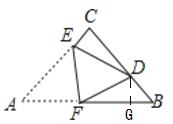
根据折叠性质,可知△AEF![]() △DEF,
△DEF,
∴AE=DE=2,AF=DF,CE=AC-AE=1,
在Rt△DCE中,由勾股定理得![]() ,
,
∴DB=![]() ;
;
在Rt△ABC中,由勾股定理得![]() ;
;
在Rt△DGB中, ![]() ,
, ![]() ;
;
设AF=DF=x,得FG=AB-AF-GB=![]() ,
,
在Rt△DFG中, ![]() ,
,
即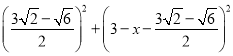 =
=![]() ,
,
解得![]() ,
,
∴![]() =
=![]() =
=![]() .
.
故答案为: ![]() .
.
点睛:主要考查了翻折变换的性质、勾股定理、锐角三件函数的定义;解题的关键是灵活运用折叠的性质、勾股定理、锐角三角函数的定义等知识来解决问题.
【题型】填空题
【结束】
18
【题目】规定:[x]表示不大于x 的最整数,(x) 表示不小于x的最小整数,[x) 表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2,则下列说法正确的是__________(写出所有正确说法).
①当x=1.7时,[x]+(x)+[x)=6;
②当x=-2.1时,[x]+(x)+[x)=-7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当-1<x<1时, 函数y=[x]+(x)+x 的图像y=4x 的图像有两个交点.
参考答案:
【答案】②③
【解析】分析:(1)根据题目中给的计算方法代入计算后判定即可;(2)根据题目中给的计算方法代入计算后判定即可;(3)根据题目中给的计算方法代入计算后判定即可;(4)结合x的取值范围,分类讨论,利用题目中给出的方法计算后判定即可.
详解:
①当x=1.7时,
[x]+(x)+[x)
=[1.7]+(1.7)+[1.7)=1+2+2=5,故①错误;
②当x=﹣2.1时,
[x]+(x)+[x)
=[﹣2.1]+(﹣2.1)+[﹣2.1)
=(﹣3)+(﹣2)+(﹣2)=﹣7,故②正确;
③当1<x<1.5时,
4[x]+3(x)+[x)
=4×1+3×2+1
=4+6+1
=11,故③正确;
④∵﹣1<x<1时,
∴当﹣1<x<﹣0.5时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当﹣0.5<x<0时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当x=0时,y=[x]+(x)+x=0+0+0=0,
当0<x<0.5时,y=[x]+(x)+x=0+1+x=x+1,
当0.5<x<1时,y=[x]+(x)+x=0+1+x=x+1,
∵y=4x,则x﹣1=4x时,得x=![]() ;x+1=4x时,得x=
;x+1=4x时,得x=![]() ;当x=0时,y=4x=0,
;当x=0时,y=4x=0,
∴当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有三个交点,故④错误,
故答案为:②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了
 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
(1)根据图中信息求出
 =___________,
=___________, =_____________;
=_____________;(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有甲、乙两个体育用品商店出售乒乓球拍和乒乓球,球拍每块价格为48元,乒乓球每个价格为2元,已知甲店制定的优惠方法是买--块球拍送6个乒乓球,乙店按总价的
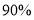 收费,某球队需要购买球拍4块,乒乓球
收费,某球队需要购买球拍4块,乒乓球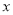 个(不少于24个).
个(不少于24个).(1)试用含有的代数式表示甲、乙两店购买球拍4块,乒乓球
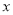 个的费用.
个的费用.(2)当需要购买240个乒乓球时,选择哪家商店购买更优惠?请说明理由.
(3)当购买多少个乒乓球时,两个商店的收费一样多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形 ABCD 中, G 为 BC 边上一点, BE AG 于 E , DF AG 于 F ,连接 DE .
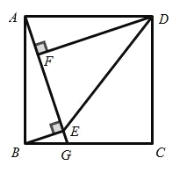
(1)求证: ABE DAF ;
(2)若 AF 1,四边形 ABED 的面积为6 ,求 EF 的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】首先,我们学习一道“最值”问题的解答:
问题:已知x>0,求
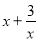 的最小值.
的最小值.解答:对于x>0,我们有:
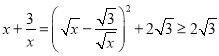
当
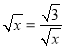 ,即
,即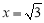 时,上述不等式取等号,所以
时,上述不等式取等号,所以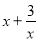 的最小值是
的最小值是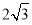
由解答知,
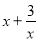 的最小值是
的最小值是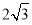 .
.弄清上述问题及解答方法之后,解答下述问题:
(1)求
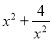 的最小值.
的最小值.(2)在直角坐标系 xOy 中,一次函数
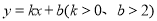 的图象与 x 轴、 y 轴分别交于 A 、 B 两点.
的图象与 x 轴、 y 轴分别交于 A 、 B 两点.①求 A 、 B 两点的坐标;
②求当OAB 的面积值等于
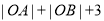 时,用b 表示 k ;
时,用b 表示 k ;③在②的条件下,求AOB 面积的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在八年级举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查30名学生的听写汉字的正确字数如下:
2
9
17
24
33
5
12
19
26
34
7
14
20
26
36
15
22
26
39
31
22
27
39
22
28
23
23
31
30
28
对这30个数据按组距8进行分组,并统计整理.
(1)请完成下面频数分布统计表;
组别
正确字数x
频数
A
0≤x<8
B
8≤x<16
C
16≤x<24
D
24≤x<32
E
32≤x<40
(2)在上图中请画出频数分布直方图;
(3)若该校八年级学生共有1200人,如果听写正确的个数少于24个定为不合格,请你估计该校八年级本次比赛听写不合格的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把所有正偶数从小到大排列,并按如下规律分组:(2)、(4,6),(8,10,12),(14,16,18,20),…,现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左往右数).如A2=(1,1),A10=(3,2),A18=(4,3),则A200可表示为( )
A.(14,9)B.(14,10)C.(15,9)D.(15,10)
相关试题

