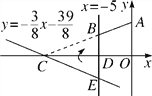
【题目】如图,在平面直角坐标系xOy中,A(0,5),直线x=-5与x轴交于点D,直线y=-![]() x-
x-![]() 与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
(1)求点C,E的坐标及直线AB的解析式;
(2)若S=S△CDE+S四边形ABDO,求S的值;
(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积,如此不更快捷吗?”但大家经反复验算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.
参考答案:
【答案】(1)C(-13,0),E(-5,-3),![]() ;(2)32;(3)见解析.
;(2)32;(3)见解析.
【解析】
(1)利用坐标轴上点的特点确定出点C的坐标,再利用直线的交点坐标的确定方法求出点E坐标,进而得到点B坐标,最后用待定系数法求出直线AB解析式;
(2)直接利用直角三角形的面积计算方法和直角梯形的面积的计算即可得出结论,
(3)先求出直线AB与x轴的交点坐标,判断出点C不在直线AB上,即可.
(1)在直线![]() 中,令y=0,则有0=
中,令y=0,则有0=![]() ,
,
∴x=﹣13,
∴C(﹣13,0),
令x=﹣5,代入![]() ,解得y=﹣3,
,解得y=﹣3,
∴E(﹣5,﹣3),
∵点B,E关于x轴对称,
∴B(﹣5,3),
∵A(0,5),
∴设直线AB的解析式为y=kx+5,
∴﹣5k+5=3,
∴k=![]() ,
,
∴直线AB的解析式为![]() ;
;
(2)由(1)知E(﹣5,﹣3),
∴DE=3,
∵C(﹣13,0),
∴CD=﹣5﹣(﹣13)=8,
∴S△CDE=![]() CD×DE=12,
CD×DE=12,
由题意知,OA=5,OD=5,BD=3,
∴S四边形ABDO=![]() (BD+OA)×OD=20,
(BD+OA)×OD=20,
∴S=S△CDE+S四边形ABDO=12+20=32;
(3)由(2)知,S=32,
在△AOC中,OA=5,OC=13,
∴S△AOC=![]() OA×OC=
OA×OC=![]() =32.5,
=32.5,
∴S≠S△AOC,
理由:由(1)知,直线AB的解析式为![]() ,令y=0,则0=
,令y=0,则0=![]() ,
,
∴x=﹣![]() ≠﹣13,
≠﹣13,
∴点C不在直线AB上,
即:点A,B,C不在同一条直线上,
∴S△AOC≠S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把边长为1厘米的6个相同正方体摆成如图的形式.
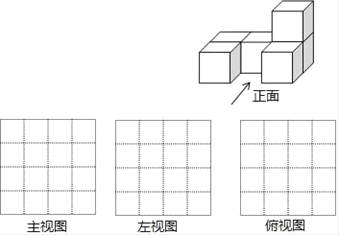
(1)画出该几何体的主视图、左视图、俯视图;
(2)直接写出该几何体的表面积为 cm2(包括底面);
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加 小正方体.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点M、N同时从原点出发沿数轴做匀速运动,己知动点M、N的运动速度比是1:2(速度单位:1个单位长度/秒),设运动时间为t秒.

(1)若动点M向数轴负方向运动,动点N向数轴正方向运动,当t=2秒时,动点M运动到A点,动点N运动到B点,且AB=12(单位长度).
①在数轴上画出A、B两点的位置,并回答:点M运动的速度是 (单位长度/秒);点N运动的速度是 (单位长度/秒).
②若点P为数轴上一点,且PA﹣PB=OP,求
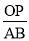 的值;
的值;(2)由(1)中A、B两点的位置开始,若M、N同时再次开始按原速运动,且在数轴上的运动方向不限,再经过几秒,MN=4(单位长度)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若有a,b两个数,满足关系式:a+b=ab﹣1,则称a,b为“共生数对”,记作(a,b).
例如:当2,3满足2+3=2×3﹣1时,则(2,3)是“共生数对”.
(1)若(x,﹣2)是“共生数对”,求x的值;
(2)若(m,n)是“共生数对”,判断(n,m)是否也是“共生数对”,请通过计算说明.
(3)请再写出两个不同的“共生数对”
-
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按下列方式搭建三角形:
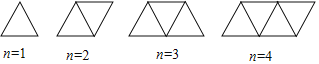
(1)当三角形个数为1时,需3根火柴棒;当三角形个数为2时,需5根火柴棒;则当三角形个数为100时,需火柴棒 根;当三角形个数为n时,需火柴棒 根(用含n的代数式表示);
(2)当火柴棒的根数为2019时,求三角形的个数?
(3)组成三角形的火柴棒能否为1000根,如果能,求三角形的个数;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.
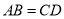 ,
,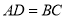 B.
B. 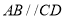 ,
,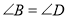
C.
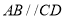 ,
,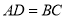 D.
D. 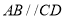 ,
,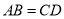
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一直角三角板MON的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
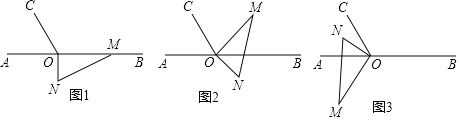
(1)求∠CON的度数;
(2)如图2是将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周的情况.在旋转的过程中,当第t秒时,三条射线OA、OC、OM构成相等的角,求此时t的值;
(3)将图1中的三角板绕点O逆时针旋转至图3,使ON在∠AOC的内部时,请探究∠AOM与∠CON的数量关系,并说明理由.
相关试题

