【题目】如图,动点M、N同时从原点出发沿数轴做匀速运动,己知动点M、N的运动速度比是1:2(速度单位:1个单位长度/秒),设运动时间为t秒.
![]()
(1)若动点M向数轴负方向运动,动点N向数轴正方向运动,当t=2秒时,动点M运动到A点,动点N运动到B点,且AB=12(单位长度).
①在数轴上画出A、B两点的位置,并回答:点M运动的速度是 (单位长度/秒);点N运动的速度是 (单位长度/秒).
②若点P为数轴上一点,且PA﹣PB=OP,求![]() 的值;
的值;
(2)由(1)中A、B两点的位置开始,若M、N同时再次开始按原速运动,且在数轴上的运动方向不限,再经过几秒,MN=4(单位长度)?
参考答案:
【答案】(1)①图详见解析,2,4;②![]() 或
或![]() ;(2)4秒或8秒或
;(2)4秒或8秒或![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)①根据题意把A、B两点表示在数轴上,计算出M、N两点的速度即可;
②设点P在数轴上对应的数为x,根据PAPB=OP,结合x的范围分情况求解即可;
(2)分情况讨论:若M、N运动的方向相同,要使得MN=4,必为N追击M;若M、N运动方向相反,要使得MN=4,必为M、N相向而行;然后根据MN=4分别列出方程求解即可..
解:(1)①∵点M、N的运动速度比是1:2,AB=12,
∴画出数轴,如图所示:
![]()
∴点M运动的速度是2(单位长度/秒);点N运动的速度是4(单位长度/秒);
②设点P在数轴上对应的数为x,
∵PA﹣PB=OP≥0,
∴x≥2,
当2≤x≤8时,PA﹣PB=(x+4)﹣(8﹣x)=x+4﹣8+x,即2x﹣4=x,解得x=4;
当x>8时,PA﹣PB=(x+4)﹣(x﹣8)=12,即x=12,
∴![]() 或
或![]() ;
;
(2)设再经过m秒MN=4(单位长度),
若M、N运动的方向相同,要使得MN=4,必为N追击M,
∴|(8﹣4m)﹣(﹣4﹣2m)|=4,即|12﹣2m|=4,
解得:m=4或m=8;
若M、N运动方向相反,要使得MN=4,必为M、N相向而行,
∴|(8﹣4m)﹣(﹣4+2m)|=4,即|12﹣6m|=4,
解得:m=![]() 或m=
或m=![]() ,
,
综上,再经过4秒或8秒或![]() 秒或
秒或![]() 秒,MN=4.
秒,MN=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.某酒厂生产A,B两种品牌的酒,平均每天两种酒共可售出600瓶,每种酒每瓶的成本和售价如表所示,设平均每天共获利y元,平均每天售出A种品牌的酒x瓶.
A
B
成本(元)
50
35
售价(元)
70
50
(1)请写出y关于x的函数关系式;
(2)如果该厂每天至少投入成本25000元,且售出的B种品牌的酒不少于全天销售总量的55%,那么共有几种销售方案?并求出每天至少获利多少元?
-
科目: 来源: 题型:
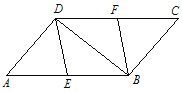
查看答案和解析>>【题目】如图,在□ABCD 中,∠ADB=90°,点 E 为 AB 边的中点,点 F 为CD 边的中点.
(1)求证:四边形 DEBF 是菱形;
(2)当∠A 等于多少度时,四边形 DEBF 是正方形?并说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把边长为1厘米的6个相同正方体摆成如图的形式.
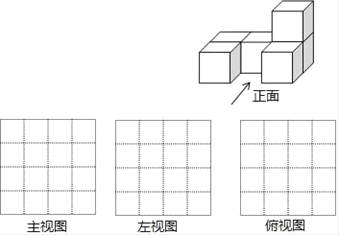
(1)画出该几何体的主视图、左视图、俯视图;
(2)直接写出该几何体的表面积为 cm2(包括底面);
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加 小正方体.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若有a,b两个数,满足关系式:a+b=ab﹣1,则称a,b为“共生数对”,记作(a,b).
例如:当2,3满足2+3=2×3﹣1时,则(2,3)是“共生数对”.
(1)若(x,﹣2)是“共生数对”,求x的值;
(2)若(m,n)是“共生数对”,判断(n,m)是否也是“共生数对”,请通过计算说明.
(3)请再写出两个不同的“共生数对”
-
科目: 来源: 题型:
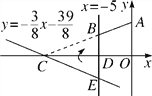
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(0,5),直线x=-5与x轴交于点D,直线y=-
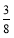 x-
x-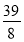 与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.(1)求点C,E的坐标及直线AB的解析式;
(2)若S=S△CDE+S四边形ABDO,求S的值;
(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积,如此不更快捷吗?”但大家经反复验算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按下列方式搭建三角形:
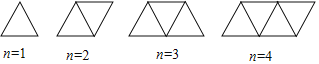
(1)当三角形个数为1时,需3根火柴棒;当三角形个数为2时,需5根火柴棒;则当三角形个数为100时,需火柴棒 根;当三角形个数为n时,需火柴棒 根(用含n的代数式表示);
(2)当火柴棒的根数为2019时,求三角形的个数?
(3)组成三角形的火柴棒能否为1000根,如果能,求三角形的个数;如果不能,请说明理由.
相关试题

