搜索
【题目】下列条件中，不能判定四边形ABCD是平行四边形的是（ ）
A. 
，
B. 
，
C. ，D. ，
参考答案：
【答案】C
【解析】
根据平行四边形的判定条件，即可判断出正确答案.
A、∵AB=CD，AD=BC，
∴四边形ABCD是平行四边形，
故A可以判断四边形ABCD是平行四边形；
B、∵AB∥CD，∴∠B+∠C=180°，
∵∠B=∠D，
∴∠D+∠C=180°，
∴AC∥BD，
∴四边形ABCD是平行四边形，
故B可以判断四边形ABCD是平行四边形；
C、∵AB∥CD，AD=BC，
∴四边形ABCD可能是平行四边形，有可能是等腰梯形．
故C不可以判断四边形ABCD是平行四边形
D、∵AB∥CD，AB=CD，
∴四边形ABCD是平行四边形，
故D可以判断四边形ABCD是平行四边形；
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若有a，b两个数，满足关系式：a+b＝ab﹣1，则称a，b为“共生数对”，记作（a，b）．
例如：当2，3满足2+3＝2×3﹣1时，则（2，3）是“共生数对”．
（1）若（x，﹣2）是“共生数对”，求x的值；
（2）若（m，n）是“共生数对”，判断（n，m）是否也是“共生数对”，请通过计算说明．
（3）请再写出两个不同的“共生数对”
-
科目： 来源： 题型：
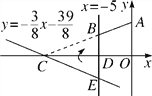
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，A(0，5)，直线x＝－5与x轴交于点D，直线y＝－
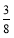x－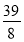
与x轴及直线x＝－5分别交于点C，E.点B，E关于x轴对称，连接AB.(1)求点C，E的坐标及直线AB的解析式；
(2)若S＝S△CDE＋S四边形ABDO，求S的值；
(3)在求(2)中S时，嘉琪有个想法：“将△CDE沿x轴翻折到△CDB的位置，而△CDB与四边形ABDO拼接后可看成△AOC，这样求S便转化为直接求△AOC的面积，如此不更快捷吗？”但大家经反复验算，发现S△AOC≠S，请通过计算解释他的想法错在哪里．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用火柴棒按下列方式搭建三角形：
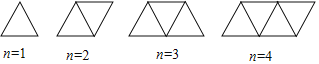
（1）当三角形个数为1时，需3根火柴棒；当三角形个数为2时，需5根火柴棒；则当三角形个数为100时，需火柴棒 根；当三角形个数为n时，需火柴棒 根（用含n的代数式表示）；
（2）当火柴棒的根数为2019时，求三角形的个数？
（3）组成三角形的火柴棒能否为1000根，如果能，求三角形的个数；如果不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，点O为直线AB上一点，过点O作射线OC，使∠AOC＝60°，将一直角三角板MON的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．
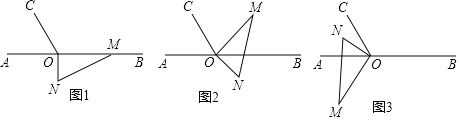
（1）求∠CON的度数；
（2）如图2是将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周的情况．在旋转的过程中，当第t秒时，三条射线OA、OC、OM构成相等的角，求此时t的值；
（3）将图1中的三角板绕点O逆时针旋转至图3，使ON在∠AOC的内部时，请探究∠AOM与∠CON的数量关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】3 月初某商品价格上涨，每件价格上涨 20%.用 3000 元买到的该商品 件数比涨价前少 20 件．3 月下旬该商品开始降价，经过两次降价后，该商品价格为每 件 19.2 元．
（1）求 3 月初该商品上涨后的价格；
（2）若该商品两次降价率相同，求该商品价格的平均降价率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】近几年购物的支付方式日益增多，某数学兴趣小组就此进行了抽样调查．调查结果显示，支付方式有：A微信、B支付宝、C现金、D其他，该小组对某超市一天内购买者的支付方式进行调查统计，得到如下两幅不完整的统计图．
请你根据统计图提供的信息，解答下列问题：
（1）本次一共调查了多少名购买者？
（2）请补全条形统计图；在扇形统计图中A种支付方式所对应的圆心角为 度．
（3）若该超市这一周内有1600名购买者，请你估计使用A和B两种支付方式的购买者共有多少名？
相关试题
