【题目】数轴上,A、B两点表示的数a,b满足|a﹣6|+(b+12)2=0
(1)a= ,b= ;
(2)若小球M从A点向负半轴运动、小球N从B点向正半轴运动,两球同时出发,小球M运动的速度为每秒2个单位,当M运动到OB的中点时,N点也同时运动到OA的中点,则小球N的速度是每秒 个单位;
(3)若小球M、N保持(2)中的速度,分别从A、B两点同时出发,经过 秒后两个小球相距两个单位长度.
![]()
参考答案:
【答案】(1)6;﹣12;(2)2.5;(3)![]() 或
或![]() 或32或40
或32或40
【解析】
(1)根据非负数的性质即可求出a、b的值;
(2)先求出M运动到OB的中点时所用的时间为6秒,再设小球N的速度是每秒x个单位,根据经过6秒N点运动到OA的中点列出方程,解方程即可;
(3)小球M向负半轴运动、小球N向正半轴运动时,分相遇前与相遇后两种情况求解;小球M、小球N都向正半轴运动时,分追上前与追上后两种情况求解.
(1)∵|a﹣6|+(b+12)2=0,
∴a﹣6=0,b+12=0,
∴a=6,b=﹣12.
故答案为6,﹣12;
(2)设M运动到OB的中点时所用的时间为t秒,
根据题意,得6﹣2t=﹣6,解得t=6.
设小球N的速度是每秒x个单位,
根据题意,得﹣12+6x=3,解得x=2.5,
答:小球N的速度是每秒2.5个单位.
故答案为2.5;
(3)若小球M、N保持(2)中的速度,分别从A、B两点同时出发,设经过y秒后两个小球相距两个单位长度.
∵A、B两点表示的数分别是6、﹣12,
∴A、B两点间的距离为6﹣(﹣12)=18.
如果小球M向负半轴运动、小球N向正半轴运动,
①相遇前:2y+2.5y=18﹣2,解得y=![]() ;
;
②相遇后:2y+2.5y=18+2,解得y=![]() ;
;
如果小球M、小球N都向正半轴运动,
①追上前:2.5y﹣2y=18﹣2,解得y=32;
②追上后:2.5y﹣2y=18+2,解得y=40.
答:若小球M、N保持(2)中的速度,分别从A、B两点同时出发,经过![]() 或
或![]() 或32或40秒后两个小球相距两个单位长度.
或32或40秒后两个小球相距两个单位长度.
故答案为![]() 或
或![]() 或32或40.
或32或40.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(11分)如图1,点A(a,b)在平面直角坐标系xOy中,点A到坐标轴的垂线段AB,AC与坐标轴围成矩形OBAC,当这个矩形的一组邻边长的和与积相等时,点A称作“垂点”,矩形称作“垂点矩形”.
(1)在点P(1,2),Q(2,-2),N(
 ,-1)中,是“垂点”的点为 ;
,-1)中,是“垂点”的点为 ;(2)点M(-4,m)是第三象限的“垂点”,直接写出m的值 ;
(3)如果“垂点矩形”的面积是
 ,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;(4)如图2,平面直角坐标系的原点O是正方形DEFG的对角线的交点,当正方形DEFG的边上存在“垂点”时,GE的最小值为8.

-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题.
程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
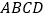 是矩形 ,
是矩形 ,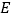 是
是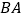 延长线上的一点,
延长线上的一点,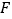 是
是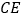 上一点,
上一点,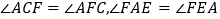 ;若
;若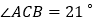 ,则
,则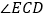 = ________ .
= ________ .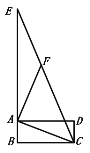
-
科目: 来源: 题型:
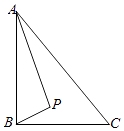
查看答案和解析>>【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A.
B.2
C.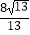
D.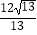
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中, ,点
,点 在边
在边 上,且
上,且 ;将
;将 沿
沿 对折至
对折至 ,延长
,延长 交边
交边 于点
于点 ,连结
,连结 ,下列结论:①.
,下列结论:①. ;②.
;②. ;③.
;③.  .其中,正确的结论有__________________.(填上你认为正确的序号)
.其中,正确的结论有__________________.(填上你认为正确的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
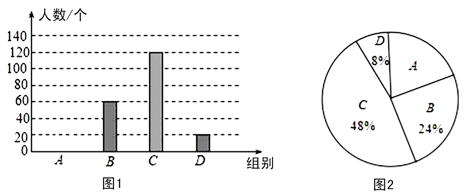
根据以上信息,回答下列问题:
(1)A组的人数是 人,并补全条形统计图;
(2)本次调查数据的中位数落在组 ;
(3)根据统计数据估计该地区25 000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有多少人.
相关试题

