【题目】已知函数y=(m+![]() )x2+(2m﹣1)x﹣3.求证:不论m为何值,该函数图象与x轴必有交点.
)x2+(2m﹣1)x﹣3.求证:不论m为何值,该函数图象与x轴必有交点.
参考答案:
【答案】证明见解析.
【解析】试题分析:一次函数图象上点的坐标特征以及抛物线与x轴的交点,分该函数为一次函数和二次函数两种情况,寻找函数图象与x轴的交点个数是解题的关键.
试题解析:
证明:当m+![]() =0,即m=﹣
=0,即m=﹣![]() 时,原函数为一次函数y=﹣
时,原函数为一次函数y=﹣![]() x﹣3,
x﹣3,
令y=﹣![]() x﹣3=0,解得:x=﹣2,
x﹣3=0,解得:x=﹣2,
∴当m=﹣![]() 时,函数y=(m+
时,函数y=(m+![]() )x2+(2m﹣1)x﹣3与x轴的交点坐标为(﹣2,0);
)x2+(2m﹣1)x﹣3与x轴的交点坐标为(﹣2,0);
当m+![]() ≠0,即m≠﹣
≠0,即m≠﹣![]() 时,该函数为二次函数,
时,该函数为二次函数,
∵△=(2m﹣1)2﹣4×(m+![]() )×(﹣3)=4m2+8m+4=4(m+1)2≥0,
)×(﹣3)=4m2+8m+4=4(m+1)2≥0,
∴函数y=(m+![]() )x2+(2m﹣1)x﹣3的图象与x轴至少有一个.
)x2+(2m﹣1)x﹣3的图象与x轴至少有一个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】红红有两把不同的锁和四把不同的钥匙,其中只有两把钥匙能打开对应的两把锁,用列表法或树状图求概率.
(1)若取一把钥匙,求红红一次打开锁的概率;
(2)若取两把钥匙,求红红恰好打开两把锁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点D的坐标是(-3,1),点A的坐标是(4,3).

(1)将△ABC平移后使点C与点D重合,点A、B与点E、F重合,画出△DEF,并直接写出E、F的坐标.
(2)若AB上的点M坐标为(x,y),则平移后的对应点M′的坐标为多少?
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点C在∠AOB的一边OA上,过点C的直线DE∥OB,CF平分∠ACD,CG⊥CF于点C.
(1)若∠O=40°,求∠ECF的度数;
(2)求证:CG平分∠OCD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来交通事故发生率逐年上升,交通问题成为重大民生问题,鄱阳二中数学兴趣小组为检测汽车的速度设计了如下实验:如图,在公路MN(近似看作直线)旁选取一点C,测得C到公路的距离为30米,再在MN上选取A、B两点,测得∠CAN=30°,∠CBN=60°.
(1)求AB的长;(精确到0.1米,参考数据
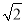 =1.41,
=1.41,  =1.73)
=1.73)(2)若本路段汽车限定速度为40千米/小时,某车从A到B用时3秒,该车是否超速?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成如下不完整的条形图和扇形图.

请结合以上信息解答下列问题:
(1)m= ;
(2)请补全上面的条形统计图;
(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为 ;
(4)已知该校共有1200名学生,请你估计该校约有 名学生最喜爱足球活动.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
相关试题

