【题目】如图,在平面直角坐标系中,点D的坐标是(-3,1),点A的坐标是(4,3).

(1)将△ABC平移后使点C与点D重合,点A、B与点E、F重合,画出△DEF,并直接写出E、F的坐标.
(2)若AB上的点M坐标为(x,y),则平移后的对应点M′的坐标为多少?
(3)求△ABC的面积.
参考答案:
【答案】(1)如图所示,△DEF即为所求,见解析;E(0,2),F(-1,0);(2)M′的坐标为(x-4,y-1);(3)△ABC的面积为![]() .
.
【解析】
(1)根据点C及其对应点D的位置知,需将△ABC先向左平移4个单位,再向下平移1个单位,据此作出点A,B的对应点,顺次连接可得三角形DEF,再根据点E、F在坐标系中的位置,写出坐标即可;
(2)根据平移规律左减右加,上加下减的规律解决问题;
(3)利用割补法求解可得.
(1)如图所示,△DEF即为所求,

由图知,E(0,2),F(-1,0);
(2)由图知,M′的坐标为(x-4,y-1);
(3)△ABC的面积为2×3-![]() ×1×2-
×1×2-![]() ×1×2-
×1×2-![]() ×1×3=
×1×3=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要把一块三角形的土地均匀分给甲、乙、丙三家农户去种植.如果∠C=90°,∠B=30°.


(1)要使这三家农户所得土地的大小、形状都相同,请你试着在图上画出来,并加以证明
(2)要使这三家农户所得土地的大小、形状仍都相同,请你试着在图上直接画出来(不用证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A(a,0),C(0,c)且满足:(a+6)2+
 =0,长方形ABCO在坐标系中(如图),点O为坐标系的原点.
=0,长方形ABCO在坐标系中(如图),点O为坐标系的原点.
(1)求点B的坐标.
(2)如图1,若点M从点A出发,以2个单位/秒的速度向右运动(不超过点O),点N从原点O出发,以1个单位/秒的速度向下运动(不超过点C),设M、N两点同时出发,在它们运动的过程中,四边形MBNO的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
(3)如图2,E为x轴负半轴上一点,且∠CBE=∠CEB,F是x轴正半轴上一动点,∠ECF的平分线CD交BE的延长线于点D,在点F运动的过程中,请探究∠CFE与∠D的数量关系,并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】红红有两把不同的锁和四把不同的钥匙,其中只有两把钥匙能打开对应的两把锁,用列表法或树状图求概率.
(1)若取一把钥匙,求红红一次打开锁的概率;
(2)若取两把钥匙,求红红恰好打开两把锁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点C在∠AOB的一边OA上,过点C的直线DE∥OB,CF平分∠ACD,CG⊥CF于点C.
(1)若∠O=40°,求∠ECF的度数;
(2)求证:CG平分∠OCD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(m+
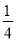 )x2+(2m﹣1)x﹣3.求证:不论m为何值,该函数图象与x轴必有交点.
)x2+(2m﹣1)x﹣3.求证:不论m为何值,该函数图象与x轴必有交点. -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来交通事故发生率逐年上升,交通问题成为重大民生问题,鄱阳二中数学兴趣小组为检测汽车的速度设计了如下实验:如图,在公路MN(近似看作直线)旁选取一点C,测得C到公路的距离为30米,再在MN上选取A、B两点,测得∠CAN=30°,∠CBN=60°.
(1)求AB的长;(精确到0.1米,参考数据
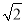 =1.41,
=1.41,  =1.73)
=1.73)(2)若本路段汽车限定速度为40千米/小时,某车从A到B用时3秒,该车是否超速?

相关试题

