搜索
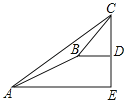
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动，如图，在点A处测得直立于地面的大树顶端C的仰角为36°，然后沿在同一剖面的斜坡AB行走13米至坡顶B处，然后再沿水平方向行走6米至大树脚底点D处，斜面AB的坡度（或坡比）i=1：2.4，那么大树CD的高度约为（参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73）（ ）
A．8.1米 B．17.2米 C．19.7米 D．25.5米
参考答案：
【答案】A．
【解析】
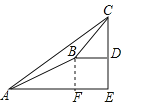
试题分析：作BF⊥AE于F，如图所示，则FE=BD=6米，DE=BF，∵斜面AB的坡度i=1：2.4，∴AF=2.4BF，设BF=x米，则AF=2.4x米，在Rt△ABF中，由勾股定理得：
，解得：x=5，∴DE=BF=5米，AF=12米，∴AE=AF+FE=18米，在Rt△ACE中，CE=AEtan36°=18×0.73=13.14米，∴CD=CE﹣DE=13.14米﹣5米≈8.1米；故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，把点P（-1，-2）向上平移4个单位长度所得点的坐标是___________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】学科内综合题：现把10个数：﹣1，23，15，12，0，﹣31，﹣11，29，43，﹣62．分别写在10张纸条上，然后把纸条放进外形，颜色完全相同的小球内，再把这10个小球放进一个大玻璃瓶中，从中任意取一球，得到正数的可能性与得到负数的可能性哪个大．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数
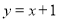的图象与反比例函数
（
为常数，且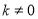
）的图象都经过点A（m，2）．
（1）求点A的坐标及反比例函数的表达式；
（2）设一次函数
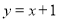的图象与x轴交于点B，若点P是x轴上一点，且满足△ABP的面积是2，直接写出点P的坐标． -
科目： 来源： 题型：
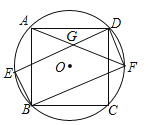
查看答案和解析>>【题目】正方形ABCD内接于⊙O，如图所示，在劣弧
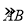上取一点E，连接DE、BE，过点D作DF∥BE交⊙O于点F，连接BF、AF，且AF与DE相交于点G，求证：（1）四边形EBFD是矩形；
（2）DG=BE．
-
科目： 来源： 题型：
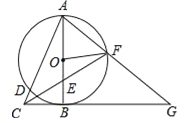
查看答案和解析>>【题目】如图，以Rt△ABC的直角边AB为直径作⊙O，交斜边AC于点D，点E为OB的中点，连接CE并延长交⊙O于点F，点F恰好落在
的中点，连接AF并延长与CB的延长线相交于点G，连接OF．（1）求证：OF=
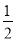BG；（2）若AB=4，求DC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠B=90°，tan∠C=
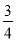，AB=6cm．动点P从点A开始沿边AB向点B以1cm/s的速度移动，动点Q从点B开始沿边BC向点C以2cm/s的速度移动．若P，Q两点分别从A，B两点同时出发，在运动过程中，△PBQ的最大面积是（ ）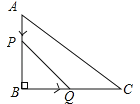
A．18cm2 B．12cm2 C．9cm2 D．3cm2
相关试题
