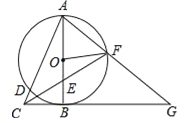
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在![]() 的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
(1)求证:OF=![]() BG;
BG;
(2)若AB=4,求DC的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)直接利用圆周角定理结合平行线的判定方法得出FO是△ABG的中位线,即可得出答案;
(2)首选得出△FOE≌△CBE(ASA),则BC=FO=![]() AB=2,进而得出AC的长,再利用相似三角形的判定与性质得出DC的长.
AB=2,进而得出AC的长,再利用相似三角形的判定与性质得出DC的长.
试题解析:(1)证明:∵以Rt△ABC的直角边AB为直径作⊙O,点F恰好落在![]() 的中点,∴
的中点,∴![]() ,∴∠AOF=∠BOF,∵∠ABC=∠ABG=90°,∴∠AOF=∠ABG,∴FO∥BG,∵AO=BO,∴FO是△ABG的中位线,∴FO=
,∴∠AOF=∠BOF,∵∠ABC=∠ABG=90°,∴∠AOF=∠ABG,∴FO∥BG,∵AO=BO,∴FO是△ABG的中位线,∴FO=![]() BG;
BG;
(2)解:在△FOE和△CBE中,∵∠FOE=∠CBE,EO=BE,∠OEF=∠CEB,∴△FOE≌△CBE(ASA),∴BC=FO=![]() AB=2,∴AC=
AB=2,∴AC=![]() =
=![]() ,连接DB,∵AB为⊙O直径,∴∠ADB=90°,∴∠ADB=∠ABC,∵∠BCD=∠ACB,∴△BCD∽△ACB,∴
,连接DB,∵AB为⊙O直径,∴∠ADB=90°,∴∠ADB=∠ABC,∵∠BCD=∠ACB,∴△BCD∽△ACB,∴![]() ,∴
,∴![]() ,解得:DC=
,解得:DC=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
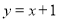 的图象与反比例函数
的图象与反比例函数 (
( 为常数,且
为常数,且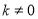 )的图象都经过点A(m,2).
)的图象都经过点A(m,2).
(1)求点A的坐标及反比例函数的表达式;
(2)设一次函数
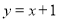 的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )
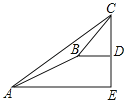
A.8.1米 B.17.2米 C.19.7米 D.25.5米
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD内接于⊙O,如图所示,在劣弧
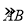 上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:(1)四边形EBFD是矩形;
(2)DG=BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=90°,tan∠C=
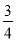 ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )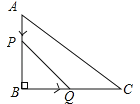
A.18cm2 B.12cm2 C.9cm2 D.3cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了传承和弘扬港口文化,我市将投入6000万元建设一座港口博物馆,其中“6000万”用科学记数法表示为( )
A.0.6×108
B.6×108
C.6×107
D.60×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )
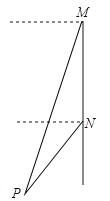
A.22.48 B.41.68 C.43.16 D.55.63
相关试题

