【题目】如图,在△ABC中, ![]() ,
, ![]() °,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至
°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至![]() ,连接
,连接![]() .已知AB
.已知AB![]() 2cm,设BD为x cm,B
2cm,设BD为x cm,B![]() 为y cm.
为y cm.
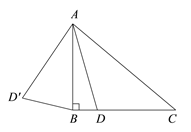
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
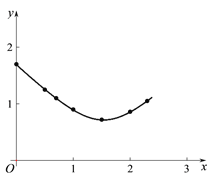
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:
线段![]() 的长度的最小值约为__________
的长度的最小值约为__________ ![]() ;
;
若![]()
![]() ,则
,则![]() 的长度x的取值范围是_____________.
的长度x的取值范围是_____________.
参考答案:
【答案】(1)0.9;(2)详见解析;(3)0.7, ![]() .
.
【解析】试题分析:
(1)观察、分析表格中的数据可知,当![]() 取0.7和2.3时,对应的
取0.7和2.3时,对应的![]() 的值是相等的,而在
的值是相等的,而在![]() 轴上0.7和2.3这两个数是关于1.5对称的,1.0和2.0也是关于1.5对称的,由此可知当
轴上0.7和2.3这两个数是关于1.5对称的,1.0和2.0也是关于1.5对称的,由此可知当![]() 时,
时, ![]() ;
;
(2)把(1)中所得结果在坐标系描出点(1.0,0.9),并用平滑的曲线连接所有描出的点,即可得到该函数的图象;
(3)①观察图象可知,该函数的图象是一根抛物线,其对称轴为直线![]() ,由此可知
,由此可知![]() 的最小值为0.7,即线段BD′的最小值约为0.7;②观察(2)中所得函数图象、分析表格中的数据可知当BD′
的最小值为0.7,即线段BD′的最小值约为0.7;②观察(2)中所得函数图象、分析表格中的数据可知当BD′![]() BD,即
BD,即![]() 时,
时, ![]() 的取值范围约为:
的取值范围约为: ![]() .
.
试题解析:
(1)∵当![]() 和
和![]() 时,
时, ![]() 的值都为
的值都为![]() ,
,
∴函数图象是这两个点是对称的,对称轴为直线![]() ,
,
又∵![]() 也是关于直线
也是关于直线![]() 对称的,
对称的,
∴当![]() 时,
时, ![]() ;
;
(2)根据(1)所得结果在坐标系描出点(1.0,0.9),并顺次用平滑曲线连接图中各点得到如下图所示的函数图象:
(3)①结合(1)、(2)可知,该函数是一个二次函数图象的一部分,其对称轴为直线![]() ,结合表格中的数据可知,
,结合表格中的数据可知, ![]() 的最小值为0.7,即线段BD′的最小值约为0.7cm;
的最小值为0.7,即线段BD′的最小值约为0.7cm;
②观察(2)中所得函数图象、分析表格中的数据可知:当BD′![]() BD,即
BD,即![]() 时,
时, ![]() 的取值范围约为:
的取值范围约为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B,C三点在⊙O上,直径BD平分∠ABC,过点D作DE∥AB交弦BC于点E,在BC的延长线上取一点F,使得EF
 DE.
DE.(1)求证:DF是⊙O的切线;
(2)连接AF交DE于点M,若 AD
 4,DE
4,DE 5,求DM的长.
5,求DM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某班体育考试跳绳项目模拟考试时10名同学的测试成绩(单位:个/分钟)
成绩(个/分钟)
140
160
169
170
177
180
人数
1
1
1
2
3
2
则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
A.方差是135B.平均数是170C.中位数是173.5D.众数是177
-
科目: 来源: 题型:
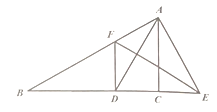
查看答案和解析>>【题目】如图所示,在
 中,
中, 是
是 平分线,
平分线, 的垂直平分线分别交
的垂直平分线分别交 延长线于点
延长线于点 .求证:
.求证: .
.
证明:∵
 平分
平分
∴

 (角平分线的定义)
(角平分线的定义)∵
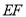 垂直平分
垂直平分
∴
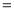 (线段垂直平分线上的点到线段两个端点距离相等)
(线段垂直平分线上的点到线段两个端点距离相等)∴
 ( )
( )∴
 (等量代换)
(等量代换)∴
 ( )
( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】某车间的甲、乙两名工人分别同时生产同种零件,在开始生产的前2个小时为生产磨合期,2个小时后有一人停工一段时间对设备进行改良升级,以提升生产效率,另一人进入正常的生产模式,他们每人生产的零件总数
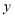 (个)与生产时间
(个)与生产时间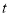 (小时)的关系如图所示,根据图象回答:
(小时)的关系如图所示,根据图象回答: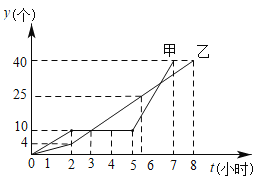
(1)在生产过程中,哪位工人对设备进行改良升级,停止生产多少小时?
(2)当
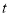 为多少时,甲、乙所生产的零件个数第一次相等?甲、乙中,谁先完成一天的生产任务?
为多少时,甲、乙所生产的零件个数第一次相等?甲、乙中,谁先完成一天的生产任务?(3)设备改良升级后每小时生产零件的个数是多少?与另一工人的正常生产速度相比每小时多生产几个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 .
.(1)该二次函数图象的对称轴是x
 ;
;(2)若该二次函数的图象开口向下,当
 时,
时,  的最大值是2,求当
的最大值是2,求当 时,
时,  的最小值;
的最小值;(3)若对于该抛物线上的两点
 ,
, 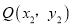 ,当
,当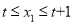 ,
,  时,均满足
时,均满足 ,请结合图象,直接写出
,请结合图象,直接写出 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题①如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;②如果三角形的三个内角的度数比是3:4:5,那么这个三角形是直角三角形;③如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形;④一个等腰直角三角形的三边是a,b,c,(a>b=c),那么a2:b2:c2=2:1:1.其中正确的是( )
A.①②B.①③C.①④D.②④
相关试题

