【题目】下列命题①如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;②如果三角形的三个内角的度数比是3:4:5,那么这个三角形是直角三角形;③如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形;④一个等腰直角三角形的三边是a,b,c,(a>b=c),那么a2:b2:c2=2:1:1.其中正确的是( )
A.①②B.①③C.①④D.②④
参考答案:
【答案】C
【解析】
分别利用勾股数的定义、勾股定理以及等腰直角三角形的边的关系分别判断得出即可.
解:①如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数,是真命题;
②如果三角形的三个内角的度数比是3:4:5,则这三角形的三个内角度数为:45°,60°,75°,因此这个三角形不是直角三角形,原命题是假命题;
③如果一个三角形的三边是12、25、21,因为![]() ,故此三角形不是直角三角形,故原命题是假命题;
,故此三角形不是直角三角形,故原命题是假命题;
④一个等腰直角三角形的三边是a,b,c,(a>b=c),那么a2:b2:c2=2:1:1,是真命题;
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,
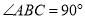 ,
, 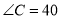 °,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至
°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至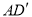 ,连接
,连接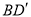 .已知AB
.已知AB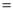 2cm,设BD为x cm,B
2cm,设BD为x cm,B 为y cm.
为y cm.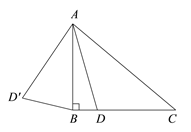
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了
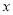 与
与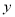 的几组值,如下表:
的几组值,如下表: 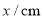
0.5
0.7
1.0
1.5
2.0
2.3

1.7
1.3
1.1
0.7
0.9
1.1
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:
线段
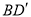 的长度的最小值约为__________
的长度的最小值约为__________ 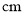 ;
;若
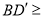
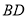 ,则
,则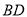 的长度x的取值范围是_____________.
的长度x的取值范围是_____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某车间的甲、乙两名工人分别同时生产同种零件,在开始生产的前2个小时为生产磨合期,2个小时后有一人停工一段时间对设备进行改良升级,以提升生产效率,另一人进入正常的生产模式,他们每人生产的零件总数
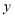 (个)与生产时间
(个)与生产时间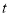 (小时)的关系如图所示,根据图象回答:
(小时)的关系如图所示,根据图象回答: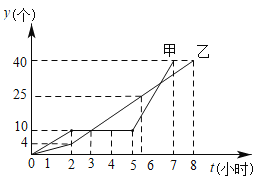
(1)在生产过程中,哪位工人对设备进行改良升级,停止生产多少小时?
(2)当
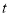 为多少时,甲、乙所生产的零件个数第一次相等?甲、乙中,谁先完成一天的生产任务?
为多少时,甲、乙所生产的零件个数第一次相等?甲、乙中,谁先完成一天的生产任务?(3)设备改良升级后每小时生产零件的个数是多少?与另一工人的正常生产速度相比每小时多生产几个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 .
.(1)该二次函数图象的对称轴是x
 ;
;(2)若该二次函数的图象开口向下,当
 时,
时,  的最大值是2,求当
的最大值是2,求当 时,
时,  的最小值;
的最小值;(3)若对于该抛物线上的两点
 ,
, 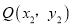 ,当
,当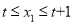 ,
,  时,均满足
时,均满足 ,请结合图象,直接写出
,请结合图象,直接写出 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是等腰直角三角形,
是等腰直角三角形, ,点
,点 是
是 的中点,延长
的中点,延长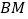 至点
至点 ,使
,使 ,连接
,连接 (如图①).
(如图①).
(1)求证:
 ≌
≌ ;
;(2)已知点
 是
是 的中点,连接
的中点,连接 (如图②).
(如图②).①求证:
 ≌
≌ ;
;②如图③,延长
 至点
至点 ,使
,使 ,连接
,连接 ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于⊙C与⊙C上的一点A,若平面内的点P满足:射线AP与⊙C交于点Q(点Q可以与点P重合),且
 ,则点P称为点A关于⊙C的“生长点”.
,则点P称为点A关于⊙C的“生长点”.已知点O为坐标原点,⊙O的半径为1,点A(-1,0).
(1)若点P是点A关于⊙O的“生长点”,且点P在x轴上,请写出一个符合条件的点P的坐标________;
(2)若点B是点A关于⊙O的“生长点”,且满足
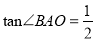 ,求点B的纵坐标t的取值范围;
,求点B的纵坐标t的取值范围;(3)直线
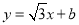 与x轴交于点M,与y轴交于点N,若线段MN上存在点A关于⊙O的“生长点”,直接写出b的取值范围是_____________________________.
与x轴交于点M,与y轴交于点N,若线段MN上存在点A关于⊙O的“生长点”,直接写出b的取值范围是_____________________________.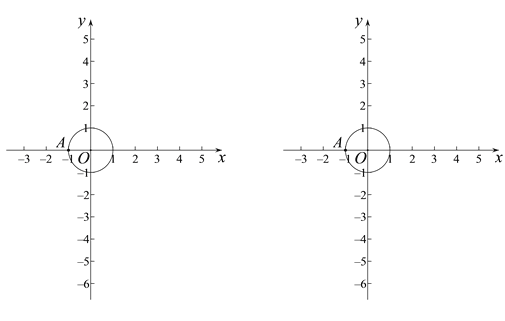
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A
 90°,AB
90°,AB AC.
AC.(1)如图1,△ABC的角平分线BD,CE交于点Q,请判断“
 ”是否正确:________(填“是”或“否”);
”是否正确:________(填“是”或“否”);(2)点P是△ABC所在平面内的一点,连接PA,PB,且PB

 PA.
PA.①如图2,点P在△ABC内,∠ABP
 30°,求∠PAB的大小;
30°,求∠PAB的大小;②如图3,点P在△ABC外,连接PC,设∠APC
 α,∠BPC
α,∠BPC β,用等式表示α,β之间的数量关系,并证明你的结论.
β,用等式表示α,β之间的数量关系,并证明你的结论.
相关试题

