【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D为△ABC内一点, ∠BAD=15°,AD=AC,CE⊥AD于E,且CE=5.
(1)求BC的长;
(2)求证:BD=CD.

参考答案:
【答案】(1)、10;(2)、证明过程见解析
【解析】
试题分析:(1)、根据等腰直角三角形的性质得出∠BAC=45°,从而得出∠CAD=30°,根据垂直得出AC=BC=10;(2)、过D作DF⊥BC于F,然后证明Rt△DCE和Rt△DCF全等,从而得出CF=CE=5,根据BC=10得出BF=FC,从而得出答案.
试题解析:(1)、在△ABC中, ∵AC=BC,∠ACB=90°,∴∠BAC=45°.
∵∠BAD=15°,∴∠CAD=30°. ∵CE⊥AD,CE=5,∴AC=10.∴BC=10.
(2)、过D作DF⊥BC于F.在△ADC中,∠CAD=30°,AD=AC,∴∠ACD=75°.
∵∠ACB=90°,∴∠FCD=15°. 在△ACE中,∠CAE=30°,CE⊥AD,∴∠ACE=60°.
∴∠ECD=∠ACD-∠ACE=15°.∴∠ECD=∠FCD.∴DF=DE.
在Rt△DCE与Rt△DCF中,![]() ∴Rt△DCE≌Rt△DCF.
∴Rt△DCE≌Rt△DCF.
∴CF=CE=5.∵BC=10,∴BF=FC. ∵DF⊥BC,∴BD=CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+3x+4交x轴于A、B两点(点A在B左边),交y轴于点C.
(1)求A、B两点的坐标;
(2)求直线BC的函数关系式;
(3)点P在抛物线的对称轴上,连接PB,PC,若△PBC的面积为4,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列推理正确的是( )
A. ∵等腰三角形是轴对称图形 ,又∵等腰三角形是等边三角形,∴等边三角形是轴对称图形
B. ∵轴对称图形是等腰三角形, 又∵等边三角形是等腰三角形,∴等边三角形是轴对称图形
C. ∵等腰三角形是轴对称图形 ,又∵等边三角形是等腰三角形,∴等边三角形是轴对称图形
D. ∵等边三角形是等腰三角形, 又∵等边三角形是轴对称图形,∴等腰三角形是轴对称图形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列四组多边形地板砖中:①正三角形与正方形;②正三角形与正六边形;③正六边形与正方形;④正八边形与正方形.将每组中的两种多边形结合,能密铺地面的是( )
A.①③④ B.②③④ C.①②③ D.①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线AB∥CD,E为直线AB、CD之间的一点.
(1)如图1,若∠B=15°,∠BED=90°,则∠D=°;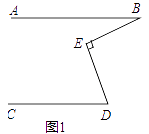
(2)如图2,若∠B=α,∠D=β,则∠BED=;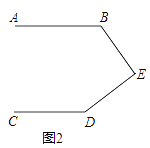
(3)如图3,若∠B=α,∠C=β,则α、β与∠BEC之间有什么等量关系?请猜想证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是真命题的是( )
A.平行四边形的四边相等B.平行四边形的对角互补
C.平行四边形是轴对称图形D.平行四边形的对角线互相平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】小华家距离县城15km,星期天8:00,小华骑自行车从家出发,到县城购买学习用品,小华与县城的距离y(km)与骑车时间x(h)之间的关系如图所示,给出以下结论:①小华骑车到县城的速度是15km/h;②小华骑车从县城回家的速度是13km/h;③小华在县城购买学习用品用了1h;④B点表示经过
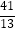 h,小华与县城的距离为15km(即小华回到家中),其中正确的结论有( )
h,小华与县城的距离为15km(即小华回到家中),其中正确的结论有( ) 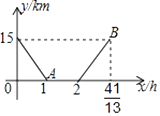
A.1个
B.2个
C.3个
D.4个
相关试题

