【题目】已知多项式x3﹣3xy2﹣4的常数是a,次数是b.
(1)则a=_____,b=_____;并将这两数在数轴上所对应的点A、B表示出来;
(2)数轴上在B点右边有一点C到A、B两点的距离之和为11,求点C在数轴上所对应的数;
(3)在数轴上是否存在点P,使P到A、B、C的距离和等于12?若存在,求点P对应的数;若不存在,请说明理由.
(4)在数轴上是否存在点P,使P到A、B、C的距离和最小?若存在,求该最小值,并求此时P点对应的数;若不存在,请说明理由.
![]()
参考答案:
【答案】(1)-4,3;(2)5;(3)P=0或![]() ;(4)点P表示的数为3时,P到A、B、C的距离和最小,最小值为9.
;(4)点P表示的数为3时,P到A、B、C的距离和最小,最小值为9.
【解析】(1)根据多项式中常数项及多项式的次数的定义即可求解;
(2)设点C在数轴上所对应的数为x,根据CA+CB=11列出方程,解方程即可;
(3)设点P在数轴上所对应的数为a,则|a+4|+|a-3|+|a-5|=12,根据绝对值的性质求解可得;
(4)点P在点A和点B(含点A和点B)之间,依此即可求解.
(1)∵多项式x3-3xy2-4的常数项是a,次数是b,
∴a=-4,b=3,
点A、B在数轴上如图所示:
![]() ,
,
故答案为:-4、3;
(2)设点C在数轴上所对应的数为x,
∵C在B点右边,
∴x>3.
根据题意得
x-3+x-(-4)=11,
解得x=5,
即点C在数轴上所对应的数为5;
(3)设点P在数轴上所对应的数为a,
则|a+4|+|a-3|+|a-5|=12,
1°、当a<-4时,-a-4+3-a+5-a=12,解得a=-![]() >-4(舍);
>-4(舍);
2°、当-4≤a<3时,a+4+a-3+5-a=12,解得a=0;
3°、当3≤a<5时,a+4+a-3+5-a=12,解得a=6>5(舍);
4°、当a≥5时,a+4+a-3+a-5=12,解得a=![]() ;
;
综上,P=0或![]() ;
;
(4)存在,点P表示的数为3,该最小值为9,
设P到A、B、C的距离和为d,
则d=|x+4|+|x-3|+|x-5|,
1°当x≤-4时,d=-x-4+3-x+5-x=-3x+4,
x=-4时,d最小=16;
2°、当-4<x≤3时,d=x+4+3-x+5-x=-x+12,
x=3时,d最小=9;
3°、当3<x≤5时,d=x+4+x-3+5-x=x+6,
x=5时,d最小=11;
4°、当x>5时,d=x+4+x-3+x-5=3x-4,此时无最小值;
综上,当点P表示的数为3时,P到A、B、C的距离和最小,最小值为9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明学了有理数的乘方后,知道23=8,25=32,他问老师,有没有20,2﹣3,如果有,等于多少?老师耐心提示他:25÷23=4,25﹣3=4,即25÷23=25﹣3=22=4,…“哦,我明白了了,”小明说,并且很快算出了答案,亲爱的同学,你想出来了吗?
(1)请仿照老师的方法,推算出20,2﹣3的值.
(2)据此比较(﹣3)﹣2与(﹣2)﹣3的大小.(写出计算过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列材料,然后解答问题.
探究:用的幂的形式表示aman的结果(m、为正整数).
根据乘方的意义,aman=
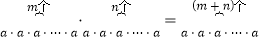 =am+n.
=am+n.(1)请根据以上结论填空:36×38= ,52×53×57= ,(a+b)3(a+b)5= ;
(2)仿照以上的分析过程,用的幂的形式表示(am)n的结果(提示:将am看成一个整体).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
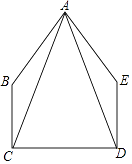
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数. -
科目: 来源: 题型:
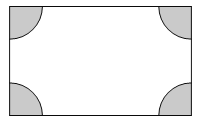
查看答案和解析>>【题目】如图,某长方形广场的四个角都有一个半径相同的四分之一圆形的草地,若圆形的半径为x米,长方形长为a米,宽为b米
(1)分别用代数式表示草地和空地的面积;
(2)若长方形长为300米,宽为200米,圆形的半径为10米,求广场空地的面积(计算结果保留到整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】用若干个大小相同,棱长为1的小正方体搭成一个几何体模型,其三视图如图所示,则搭成这个几何体模型所用的小正方体的个数是( )

A. 4 B. 5 C. 6 D. 7
相关试题

