【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=![]() 则∠BOC=_______,∠AOM=_______,∠BON=_________;
则∠BOC=_______,∠AOM=_______,∠BON=_________;
(2)若∠AOC=![]() 则∠BON=_______(用含有
则∠BON=_______(用含有![]() 的式子表示);
的式子表示);
(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变,若∠AOC=![]() (
(![]() 为钝角),求∠BON的度数(用含
为钝角),求∠BON的度数(用含![]() 的式子表示).
的式子表示).

参考答案:
【答案】(1)59°40′; 29°20′; 60°40′; (2)2α;
(3)360°-2α.
【解析】
(1)根据∠BOC=∠AOB-∠AOC进行计算即可,
由OC平分∠MOB得∠BOM=2∠BOC,则∠AOM=∠BOM-∠AOB,
∠BON=180°-∠BOM,代入计算即可得出答案;
(2)仿照(1)中方法,先求出∠BOC,再求得∠BOM,最后再代入∠BON=180°-∠BOM化简即可;
(3)由图可知∠BOC=∠AOC-∠AOB,然后由角平分线定义得∠BOM=2∠BOC,最后代入∠BON=180°-∠BOM化简即可得出答案.
解:(1)∠BOC=∠AOB-∠AOC
=90°-30°20′
=59°40′,
∵OC平分∠MOB,
∴∠BOM=2∠BOC=2×59°40′=119°20′,
∴∠AOM=∠BOM-∠AOB
=119°20′-90°
=29°20′,
∠BON=180°-∠BOM
=180°-119°20′
=60°40′.
故答案为:59°40′,29°20′,60°40′;
(2)∠BOC=∠AOB-∠AOC=90°-α,
∵OC平分∠MOB,
∴∠BOM=2∠BOC=2(90°-α)=180°-2α,
∴∠BON=180°-∠BOM
=180°-(180°-2α)
=2α.
故答案为:2α;
(3)由图可知∠BOC=∠AOC-∠AOB=α-90°,
∵OC平分∠MOB,
∴∠BOM=2∠BOC=2(α-90°)= 2α-180°,
∴∠BON=180°-∠BOM
=180°-(2α-180°)
=360°-2α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前全国提倡环保,节能灯在城市已基本普及,某商场计划购进甲、乙两种节能灯共1000只,这两种节能灯的进价,售价如下表:
进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)如何进货,进货款恰好为37000元?
(2)为确保乙型节能灯顺利畅销,在(1)的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为20%,请问乙型节能灯需打几折?
-
科目: 来源: 题型:
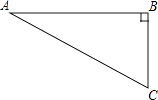
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
A.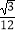
B.
C.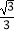
D.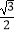
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣1)2016+2sin60°﹣|﹣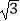 |+π0;
|+π0;
(2)(x﹣1)2﹣2(x﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣3mx+2(m﹣1)=0的两根为x1、x2 , 且
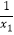 +
+ 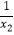 =﹣
=﹣  ,则m的值是多少?
,则m的值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=8(点A在点B的左侧)
(1)若在直线AB上取一点C,使得AC=3CB,点D是CB的中点,求AD的长;
(2)若M是线段AB的中点,点P是线段AB延长线上任意一点,请说明PA+PB﹣2PM是一个定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某快递公司针对新客户优惠收费,首件物品的收费标准为:若重量不超过10千克,则免运费;当重量为
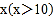 千克时,运费为
千克时,运费为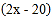 元;第二件物品的收费标准为:当重量为
元;第二件物品的收费标准为:当重量为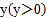 千克时,运费为
千克时,运费为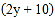 元。
元。(1)若新客户所奇首件物品的重量为13千克,则运费是多少元?
(2)若新客户所寄首件物品的运费为32元,则物品的重量是多少千克?
(3)若新客户所寄首件物品与第二件物品的重量之比为2:5,共付运费为60元,则两件物品的重量各是多少千克?
相关试题

