【题目】某快递公司针对新客户优惠收费,首件物品的收费标准为:若重量不超过10千克,则免运费;当重量为![]() 千克时,运费为
千克时,运费为![]() 元;第二件物品的收费标准为:当重量为
元;第二件物品的收费标准为:当重量为![]() 千克时,运费为
千克时,运费为![]() 元。
元。
(1)若新客户所奇首件物品的重量为13千克,则运费是多少元?
(2)若新客户所寄首件物品的运费为32元,则物品的重量是多少千克?
(3)若新客户所寄首件物品与第二件物品的重量之比为2:5,共付运费为60元,则两件物品的重量各是多少千克?
参考答案:
【答案】(1)6元;(2)26千克;(3)首件物品的重量为10千克,第二件物品的重量为25千克.
【解析】
(1)根据新客户所寄首件物品的重量为x千克(x>10)时,运费为(2x-20)元,把x=13代入2x-20,计算即可求解;
(2)根据快递公司针对新客户首件物品的收费标准,可知2x-20=32,解方程即可求解;
(3)设首件物品的重量为2a千克,则第二件物品的重量为5a千克,分①0<2a≤10;②2a>10两种情况进行讨论.
解:(1)∵13>10,
∴运费为:2×13-20=6(元).
答:若新客户所寄首件物品的重量为13千克,则运费是6元;
(2)由题意,得2x-20=32,
解得x=26.
答:若新客户所寄首件物品的运费为32元,则物品的重量是26千克;
(3)设首件物品的重量为2a千克,则第二件物品的重量为5a千克.
①当0<2a≤10,即0<a≤5时,
2×5a+10=60,解得a=5,
此时2a=10,5a=25;
②当2a>10,即a>5时,
2×2a-20+2×5a+10=60,解得a=5,
a不大于5,
∴此情况不符合题意,舍去.
综上,首件物品的重量为10千克,第二件物品的重量为25千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=
 则∠BOC=_______,∠AOM=_______,∠BON=_________;
则∠BOC=_______,∠AOM=_______,∠BON=_________;(2)若∠AOC=
 则∠BON=_______(用含有
则∠BON=_______(用含有 的式子表示);
的式子表示);(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变,若∠AOC=
 (
( 为钝角),求∠BON的度数(用含
为钝角),求∠BON的度数(用含 的式子表示).
的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣3mx+2(m﹣1)=0的两根为x1、x2 , 且
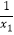 +
+ 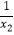 =﹣
=﹣  ,则m的值是多少?
,则m的值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=8(点A在点B的左侧)
(1)若在直线AB上取一点C,使得AC=3CB,点D是CB的中点,求AD的长;
(2)若M是线段AB的中点,点P是线段AB延长线上任意一点,请说明PA+PB﹣2PM是一个定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义[x]表示不超过实数x的最大整数,如[1.8]=1,[﹣1.4]=﹣2,[﹣3]=﹣3.函数y=[x]的图象如图所示,则方程[x]=
 x2的解为( )#N.
x2的解为( )#N.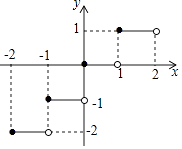
A.0或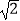
B.0或2
C.1或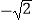
D.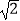
或﹣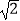
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市准备购进甲、乙两种品牌的文具盒,甲、乙两种玩具盒的进价和售价如下表,预计购进乙品牌文具盒的数量y(个)与甲品牌玩具盒数量x(个)之间的函数关系如图所示.
甲
乙
进价(元)
15
30
售价(元)
20
38
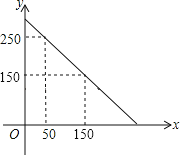
(1)y与x之间的函数关系式是 ;
(2)若超市准备用不超过6000元购进甲、乙两种文具盒,则至少购进多少个甲种文具盒?
(3)在(2)的条件下,写出销售所得的利润W(元)与x(个)之间的关系式,并求出获得的最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则AB+AD的值是( )
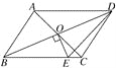
A. 10
B. 15
C. 25
D. 30
相关试题

