搜索
【题目】如图，在正方形ABCD中，E是BC的中点，F是CD上一点，且CF=
CD，求证：∠AEF=90°．
参考答案：
【答案】证明见解析.
【解析】试题分析：利用正方形的性质得出AB=BC=CD=DA，∠B=∠C=∠D=90°，设出边长为a，进一步利用勾股定理求得AE、EF、AF的长，再利用勾股定理逆定理判定即可．
试题解析：证明：∵ABCD为正方形，∴AB=BC=CD=DA，∠B=∠C=∠D=90°．设AB=BC=CD=DA=a．∵E是BC的中点，且CF=
CD，∴BE=EC=
a，CF=a．在Rt△ABE中，由勾股定理可得：AE2=AB2+BE2=
a2，同理可得：EF2=EC2+FC2=
a2，AF2=AD2+DF2=
a2．∵AE2+EF2=AF2，∴△AEF为直角三角形，∴∠AEF=90°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】函数 y=
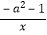（a为常数）的图象上有三点（﹣4，y1），（﹣1，y2），（2，y3），则函数值y1 ， y2 ， y3的大小关系是（ ）
A.y3＜y1＜y2
B.y3＜y2＜y1
C.y1＜y2＜y3
D.y2＜y3＜y1 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线l1：y=
（x﹣2）2﹣2与x轴分别交于O、A两点，将抛物线l1向上平移得到l2 ， 过点A作AB⊥x轴交抛物线l2于点B，如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16，则抛物线l2的函数表达式为（ ）
A.y=（x﹣2）2+4
B.y=（x﹣2）2+3
C.y=（x﹣2）2+2
D.y=（x﹣2）2+1 -
科目： 来源： 题型：
查看答案和解析>>【题目】一个口袋中有1个黑球和若干个白球，这些球除颜色外其他都相同．已知从中任意摸取一个球，摸得黑球的概率为
．
（1）求口袋中白球的个数；
（2）如果先随机从口袋中摸出一球，不放回，然后再摸出一球，求两次摸出的球都是白球的概率．用列表法或画树状图法加以说明． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，菱形ABCD中，DE⊥AB于E，DF⊥BC于F．
（1）求证：△ADE≌△CDF；
（2）若∠EDF=50°，求∠BEF的度数．
-
科目： 来源： 题型：
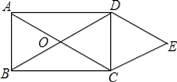
查看答案和解析>>【题目】如图，O为矩形ABCD对角线的交点，DE∥AC，CE∥BD．
（1）求证：四边形OCED是菱形．
（2）若AB=6，BC=8，求四边形OCED的周长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，BC=26cm，动点P从点A出发沿AD方向向点D以1cm/s的速度运动，动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动．点P、Q分别从点A和点C同时出发，当其中一点到达端点时，另一点随之停止运动．
（1）经过多长时间，四边形PQCD是平行四边形？
（2）经过多长时间，四边形PQBA是矩形？
（3）经过多长时间，当PQ不平行于CD时，有PQ=CD．
相关试题
