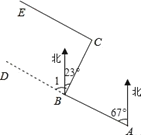
【题目】如图,某工程队从A点出发,沿北偏西67°方向修一条公路AD,在BD路段出现塌陷区,就改变方向,由B点沿北偏东23°的方向继续修建BC段,到达C点又改变方向,从C点继续修建CE段,∠ECB应为多少度,可使所修路段CE∥AB?试说明理由.此时CE与BC有怎样的位置关系?
以下是小刚不完整的解答,请帮他补充完整.
解:由已知平行,得∠1=∠A=67°(两直线平行, )
∴∠CBD=23°+67°= °,
当∠ECB+∠CBD= °时,
可得CE∥AB.( )
所以∠ECB= °
此时CE⊥BC.( )
参考答案:
【答案】同位角相等;90;180;同旁内角互补,两直线平行;90;垂直定义.
【解析】
根据平行线的性质推出∠1=∠A=67°,求出∠DBC=90°,根据平行线的判定得出当∠ECB+∠CBD=180°时AB∥CE,再求出即可.
解:由已知平行,得∠1=∠A=67°(两直线平行,同位角相等),
∴∠CBD=23°+67°=90°,
当∠ECB+∠CBD=180°时,
可得CE∥AB.( 同旁内角互补,两直线平行)
所以∠ECB=90°,
此时CE⊥BC(垂直定义),
故答案为:同位角相等;90;180;同旁内角互补,两直线平行;90;垂直定义.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点
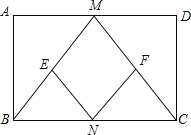
(1)求证:△ABM≌△DCM
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB= _时,四边形MENF是正方形(只写结论,不需证明)
-
科目: 来源: 题型:
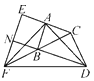
查看答案和解析>>【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N.
(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程是关于x的一元二次方程的是( )
A. ax2+bx+c=0 B.
 =2 C. x2+2x=y2-1 D. 3(x+1)2=2(x+1)
=2 C. x2+2x=y2-1 D. 3(x+1)2=2(x+1) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取
 进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:运动项目
频数(人数)
羽毛球
30
篮球


乒乓球
36
排球

足球
12

请根据以上图表信息解答下列问题:
(1)频数分布表中的
 ,
, ;
;(2)在扇形统计图中,“排球”所在的扇形的圆心角为 度;
(3)全校有多少名学生选择参加乒乓球运动?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售每台进价分别为190元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
1770元
第二周
4台
10台
3060 元
(进价、售价均保持不变,利润=销售收入一进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5300元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标,若能,请给出相应的采购方案;若不能,请说明理由.
相关试题

