【题目】如图,抛物线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点,其中
两点,其中![]() 、
、![]() 是方程的
是方程的![]() 两根,且
两根,且![]() .
.
(![]() )求抛物线的解析式;
)求抛物线的解析式;
(![]() )直线
)直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形.若存在,求所有
为直角三角形.若存在,求所有![]() 点坐标;反之说理;
点坐标;反之说理;
(![]() )点
)点![]() 为
为![]() 轴上方的抛物线上的一个动点(
轴上方的抛物线上的一个动点(![]() 点除外),连
点除外),连![]() 、
、![]() ,若设
,若设![]() 的面积为
的面积为![]() .
. ![]() 点横坐标为
点横坐标为![]() ,则
,则![]() 在何范围内时,相应的点
在何范围内时,相应的点![]() 有且只有
有且只有![]() 个.
个.

参考答案:
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)解方程求得抛物线与x轴交点的横坐标,再用待定系数法求抛物线的解析式即可;(2)用待定系数法求得直线AC的解析式,再分①∠DBC=90°、②∠DBC=90°两种情况求点D的坐标即可;(3)求得点P在抛物线AB段上时S的最大值,再求得点P在抛物线AC段上时,S的最大值,即可得S的取值范围.
试题解析:
(![]() )
)![]() ,
,
![]() ,
, ![]() ,
,
设![]() ,
,
把![]() 代入得,
代入得, ![]() ,
,
解得![]() .
.
∴![]()
![]() .
.
(![]() )设直线AC的解析式为y=kx+b,将A、C两点坐标代入得,
)设直线AC的解析式为y=kx+b,将A、C两点坐标代入得,
![]() ,
,
解得 ,k=![]() ,b=4 ,
,b=4 ,
∴![]() .
.
①∠BDC=90°时,
![]() .
.
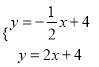 ,
, ![]() ,
,
∴![]() .
.
②∠DBC=90°时,x=-2,y=-![]() ×(-2)+4=5,则D点坐标为(-2,5);
×(-2)+4=5,则D点坐标为(-2,5);
∴![]() ,
, ![]() .
.

(3)点P在抛物线AC段上时S最大值为16,点P在抛物线AB段上时S最大值为20,
则S的取值范围为16<S<20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一个三角形,分别连接这个三角形三边的中点得到图②;再分别连接图②中间小三角形三边的中点,得到图③.

(1)图②有_____个三角形;图③有_____个三角形.
(2)按上面的方法继续下去,第
 个图形中有 个三角形?
个图形中有 个三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】作图,思考并回答问题:如图,已知:ABC
(1)按下列要求作图:取边AB、AC的中点D、E,连结线段DE;
(2)用刻度尺测量线段 DE、BC的长度分别为 ;
(3)用量角器得
 B与
B与 ADE的度数分别为 ;
ADE的度数分别为 ;(4)通过(2)、(3)你发现DE与BC什么关系?请写出你的猜想.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,BM是∠ABC的平分线,交CD于点M,且DM=2,平行四边形ABCD的周长是14,则BC的长等于( )

A. 2B. 2.5C. 3D. 3.5
-
科目: 来源: 题型:
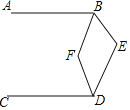
查看答案和解析>>【题目】如图,
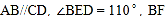 平分
平分 平分
平分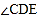 ,则
,则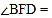 ______ .
______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+2x﹣3,
(1)用描点法画出y=x2+2x﹣3的图象.
(2)根据你所画的图象回答问题:当x 时,函数值y随x的增大而增大,当x 时,函数值y随x的增大而减小.
解:列表得:
X
Y
描点、连线

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一块长16m,宽12m的矩形荒地上建造一个花园,要求花轩占地面积为荒地面积的一半,下面分别是小强和小颖的设计方案.
(1)你认为小强的结果对吗?请说明理由.

(2)请你帮助小颖求出图中的x.
(3)你还有其他的设计方案吗?请在图(3)中画出一个与图(1)(2)有共同特点的设计草图,并加以说明.

相关试题

