【题目】如图,在平行四边形ABCD中,BM是∠ABC的平分线,交CD于点M,且DM=2,平行四边形ABCD的周长是14,则BC的长等于( )

A. 2B. 2.5C. 3D. 3.5
参考答案:
【答案】B
【解析】
由平行四边形的性质可得AB∥DC,易得∠CMB=∠ABM,再结合角平分线定义可得∠ABM=∠CBM,则有∠CMB=∠ABM=∠CBM;接下来利用等角对等边的性质可得BC=MC,然后结合已知平行四边形的周长进行计算,即可求出DM的长.
∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠CMB=∠ABM.
∵BM平分∠ABC,
∴∠ABM=∠CBM,
∵∠ABM=∠CBM,∠CMB=∠ABM,
∴∠CMB=∠ABM=∠CBM,
∴MC=BC.
∵![]() ABCD的周长是14,
ABCD的周长是14,
∴BC+CM+DM=7,
∵DM=2,
∴BC=(7-2) ÷2=2.5.
故选B.
-
科目: 来源: 题型:
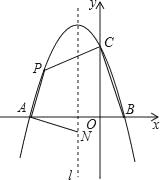
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,
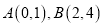 ,将线段
,将线段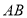 平移得到线段
平移得到线段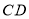 ,点
,点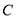 的坐标为
的坐标为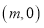 ,连结
,连结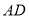 .
.(1)点
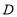 的坐标为__________________(用含
的坐标为__________________(用含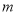 的式子表示);
的式子表示);(2)若
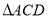 的面积为4,求点
的面积为4,求点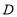 的坐标;
的坐标;(3)如图2,在(2)的条件下,延长
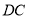 交
交 轴于点
轴于点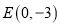 ,延长
,延长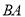 交
交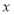 轴于
轴于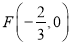 ,
, 是
是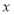 轴上一动点,
轴上一动点,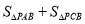 的值记为
的值记为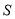 ,在点
,在点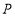 运动的过程中,
运动的过程中,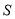 的值是否发生变化,若不变,请求出
的值是否发生变化,若不变,请求出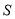 的值,并写出此时
的值,并写出此时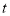 的取值范围,若变化,说明理由.
的取值范围,若变化,说明理由.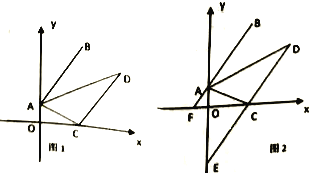
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在等边三角形ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
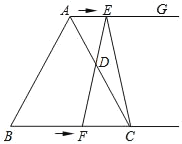
(1)连接EF,当EF经过AC边的中点D时,求证:四边形AFCE是平行四边形;
(2)填空:①当t为 s时,四边形ACFE是菱形;②当t为 s时,△ACE的面积是△ACF的面积的2倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
 ,
, 分别在直线
分别在直线 上,
上, 是平面内一点,
是平面内一点, 和
和 的平分线所在直线相交于点
的平分线所在直线相交于点 .
.(1)如图1,当
 都在直线
都在直线 之间,且
之间,且 时,
时, 的度数为_________;
的度数为_________;(2)如图2,当
 都在直线
都在直线 上方时,探究
上方时,探究 和
和 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;(3)如图3,当
 在直线
在直线 两侧时,直接写出
两侧时,直接写出 和
和 之间的数量关系是_____.
之间的数量关系是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠CAB=2∠B,AE平分∠CAB,CD⊥AB于D,AC=3,AD=1.下列结论:①∠AEC=∠CAB;②EF=CE;③AC=AE;④BD=4;

正确的是___________(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于
 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
A. 2 B. 4 C. 6 D. 8
相关试题

