【题目】为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益p(元)会相应降低且满足:p=﹣ ![]() x+110(x≥0).
x+110(x≥0). 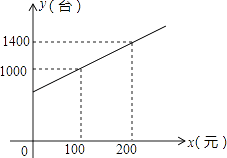
(1)在政府补贴政策实施后,求出该商场销售彩电台数y与政府补贴款额x之间的函数关系式;
(2)在政府未出台补贴措施之前,该商场销售彩电的总收益额为多少元?
(3)要使该商场销售彩电的总收益最大,政府应将每台补贴款额x定为多少?并求出总收益的最大值.
参考答案:
【答案】
(1)解:根据题意,可设y=kx+b
将(100,1000),(200,1400)代入上式,得: ![]() ,
,
解得 ![]() ,
,
故所求作的函数关系式为:y=4x+600
(2)解:∵在y=4x+600中,当x=0时,y=600,
在 ![]() 中,当x=0时,p=110
中,当x=0时,p=110
∴600×110=66000
答:在政府未出台补贴措施之前,该商场销售彩电的总收益额为66000元
(3)解:设总收益为W元,则
W= ![]()
= ![]()
= ![]()
∵ ![]() ,
,
∴W存在最大值,
∴当x=200时W有最大值98000.
答:政府应将每台补贴款额定为200元时,可获得最大利润98000元
【解析】(1)根据题意,可设y=kx+b,将(100,1000),(200,1400)代入上式,即可解决问题.(2)分别求出销售台数,每台的利润,即可解决问题.(3)构建二次函数,然后利用配方法确定函数最值问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).
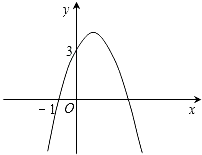
(1)求出b,c的值,并写出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
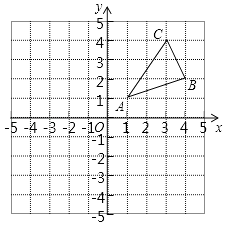
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;并写出点A2、B2、C2坐标;
(3)请画出△ABC绕O顺时针旋转90°后的△A3B3C3;并写出点A3、B3、C3坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.

(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点 E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.

(1)求E点坐标;
(2)设抛物线的解析式为y=a(x﹣h)2+k,求a,h,k;
(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点M,N的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形
 的边长为4,边
的边长为4,边 在
在 轴上,边
轴上,边 在
在 轴上,点
轴上,点 是
是 轴上一点,坐标为
轴上一点,坐标为 ,点
,点 为
为 的中点,连接
的中点,连接 .
.(1)点
 的坐标为;
的坐标为;(2)判断
 的形状,并证明你的结论.
的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于点E,∠E=30°,交AB于点D,连接AE,则SADC:S△ADE的比值为( )
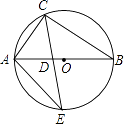
A.
B.
C.
D.1
相关试题

