Question

【题目】如图所示，正三角形ABC的边长为3＋.

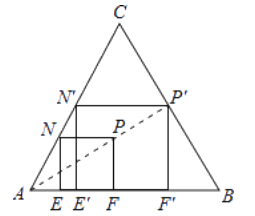
(1)如图，正方形EFPN的顶点E，F在边AB上，顶点N在边AC上，在正三角形ABC及其内部，以点A为位似中心，作正方形EFPN的位似正方形E′F′P′N′，且使正方形E′F′P′N′的面积最大(不要求写作法)；

(2)求(1)中作出的正方形E′F′P′N′的面积．

Answer 1

【答案】(1)见解析;(2) 36－18.

【解析】

（1）利用位似图形的性质，作出正方形EFPN的位似正方形E′F′P′N′，如图所示；

（2）根据正三角形、正方形、直角三角形相关线段之间的关系，利用等式E′F′+AE′+BF′=AB，列方程求得正方形E′F′P′N′的边长，即可求解.

（1）如图，正方形E′F′P′N′即为所求.

（2）设正方形E′F′P′N′的边长为x，

∵△ABC为正三角形，

∴AE′=BF′=x.

∵E′F′+AE′+BF′=AB，

∴x+x+x=3+，

∴x=，即x=3-3.

故（1）中作出的正方形E′F′P′N′的边长3-3,

则E′F′P′N′的面积为：(3-3)= 36－18.