搜索
【题目】如图，在平面直角坐标系中，四边形OABC是菱形，点C的坐标为（4，0），∠AOC=60°，垂直于x轴的直线l从y轴出发，沿x轴正方向以每秒1个单位长度的速度向右平移，设直线l与菱形OABC的两边分别交于点M，N（点M在点N的上方），若△OMN的面积为S，直线l的运动时间为t 秒（0≤t≤4），则能大致反映S与t的函数关系的图象是（ ）
A.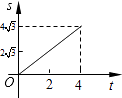
B.
C.
D.
参考答案：
【答案】C
【解析】解：过A作AD⊥x轴于D，
∵OA=OC=4，∠AOC=60°，
∴OD=2，
由勾股定理得：AD=2 
，
①当0≤t＜2时，如图所示，ON=t，MN= ON= t，S= 
ONMN= 
t2；
②2≤t≤4时，ON=t，MN=2 ，S= ON2 = t．
故选：C．
【考点精析】关于本题考查的函数的图象和菱形的性质，需要了解函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在△ABC中，∠A=90
（1）请用圆规和直尺作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切（保留作图痕迹，不写作法和证明）．
（2）若∠B=60，AB=3，求⊙P的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】“大美湿地，水韵盐城”．某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生，要求每位同学选择且只能选择一个最想去的景点，下面是根据调查结果进行数据整理后绘制出的不完整的统计图：
请根据图中提供的信息，解答下列问题：
（1）求被调查的学生总人数；
（2）补全条形统计图，并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数；
（3）若该校共有800名学生，请估计“最想去景点B“的学生人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上，这四条直线中相邻两条之间的距离依次为h1、h2、h3 ． 若h1=2，h2=1，则正方形ABCD的面积为（ ）
A.9
B.10
C.13
D.25 -
科目： 来源： 题型：
查看答案和解析>>【题目】某公司欲招聘一名公关人员，对甲、乙两位候选人进行了面试和笔试，他们的成绩如下表所示：
如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权．则( )
A. 甲的平均成绩高于乙的平均成绩
B. 乙的平均成绩高于甲的平均成绩
C. 甲与乙的平均成绩相同
D. 无法确定谁的成绩更高
-
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂为了选择1名车工参加加工直径为10 mm的精密零件的技术比赛，随机抽取甲、乙两名车工加工的5个零件，现测得的结果如下表，请你比较
、
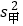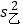的大小( )
A.
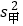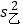
＞B.
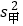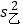
＝C.
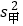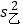
＜D.
≤ -
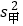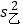
科目： 来源： 题型：
查看答案和解析>>【题目】某公司33名职工的月工资(单位：元)如下：
(1)求该公司职工月工资的平均数、中位数、众数；(精确到个位)
(2)假设副董事长的工资从5 000元提升到20 000元，董事长的工资从5 500元提升到30 000元，那么新的平均数、中位数、众数又各是多少？(精确到个位)
(3)你认为哪个统计量更能反映这个公司职工的工资水平,并说明理由．
相关试题
