【题目】如图AB∥CD,点P是平面内直线AB、CD外一点连接PA、PC。
(1)写出所给的四个图形中∠APC、∠PAB、∠PCD之间的数量关系;
(2)证明图(1)和图(3)的结论。

参考答案:
【答案】(1)图1,∠APC+∠A+∠C=360°;图2,∠APC=∠A+∠C;图3,∠C=∠A+∠APC;图4,∠A=∠C+∠APC;(2)证明图1见解析;证明图3见解析.
【解析】
1)依据图形可得∠APC、∠PAB、∠PCD之间的数量关系;
(2)过P作PE∥AB,即可得到PE∥CD,再根据平行线的性质以及角的和差关系,即可得出∠PCD=∠CPE,∠PAB=∠APE,利用三角形的外角的性质,得出∠C=∠A+∠APC.
(1)图1,∠APC+∠A+∠C=360°;图2,∠APC=∠A+∠C;图3,∠C=∠A+∠APC;图4,A=∠C+∠APC.
(2)证明图1:

如图,过P点作,PE∥AB,则:∠A+∠APE=180°,
∵AB∥CD,
∴PE∥CD
∴∠EPC+∠C=180°.
又∵∠APC=∠APE+∠EPC,
∴∠APC+∠A+∠C=360°;
证明图3:过P作PE∥AB,
∵AB∥CD,
∴PE∥CD,
∴∠PCD=∠CPE,∠PAB=∠APE,
∴∠APC=∠CPE-∠APE=∠C-∠A,即∠C=∠A+∠APC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图小方格的边长为1个单位。
(1)画出坐标系,使A、B的坐标分别为(1,1)、(-2,0),并写出点C的坐标;
(2)若将△ABC向右平移4个单位,再向上平移3个单位,得到
 ,在图中画出
,在图中画出 ;
;(3)写出△ABC的面积.

-
科目: 来源: 题型:
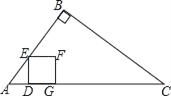
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点D从点A出发以1cm/s的速度运动到点C停止.作DE⊥AC交边AB或BC于点E,以DE为边向右作正方形DEFG.设点D的运动时间为t(s).
(1)求AC的长.
(2)请用含t的代数式表示线段DE的长.
(3)当点F在边BC上时,求t的值.
(4)设正方形DEFG与△ABC重叠部分图形的面积为S(cm2),当重叠部分图形为四边形时,求S与t之间的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛是古代的一种容量位),1个大桶加上5个小桶可以盛酒2斛。
(1)1个大桶、1个小桶分别可以盛酒多少斛?
(2)盛酒16斛,需要大桶、小桶各多少?(写出两种方案即可)
-
科目: 来源: 题型:
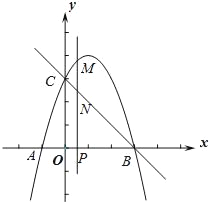
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(1)求抛物线的解析式和直线BC的解析式;
(2)当点P在线段OB上运动时,若△CMN是以MN为腰的等腰直角三角形时,求m的值;
(3)当以C、O、M、N为顶点的四边形是以OC为一边的平行四边形时,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在平面直角坐标系xOy中,函数y=
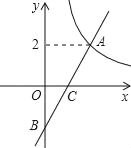
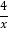 (x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).(1)求一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,若P是x轴上一点,且满足△PAB的面积是6,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )

A.2B.2.5或3.5
C.3.5或4.5D.2或3.5或4.5
相关试题

