【题目】在乘法公式的学习中,我们采用了构造几何图形的方法研究问题,借助直观、形象的几何模型,加深对乘法公式的认识和理解,从中感悟数形结合的思想方法,感悟几何与代数内在的统一性,根据课堂学习的经验,解决下列问题:
(1)如图①边长为(x+3)的正方形纸片,剪去一个边长为x的正方形之后,剩余部分可拼剪成一个长方形(不重叠无缝隙),则这个长方形的面积为 (用含x的式子表示).
(2)如果你有5张边长为a的正方形纸,4张长、宽分别为a、b(a>b)的长方形纸片,3张边长为b正方形纸片.现从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(不重叠无缝隙),则拼成的正方形的边长最长可以为
A.a+b;B.a+2b;C.a+3b;D.2a+b.
(3)1个大正方形和4个大小完全相同的小正方形按图②③两种方式摆放,求图③中,大正方形中未被4个小正方形覆盖部分的面积.(用含m、n的代数式表示)

参考答案:
【答案】(1)![]() (2)D (3)
(2)D (3)![]()
【解析】
(1)两个正方形的面积差就是长方形的面积;
(2)根据5张边长为a的正方形纸片的面积是5a2,4张边长分别为a、b(a>b)的矩形纸片的面积是4ab,3张边长为b的正方形纸片的面积是3b2,得出4a2+4ab+b2=(2a+b)2,再根据正方形的面积公式即可得出答案;
(3)利用大正方形的面积减去4个小正方形的面积即可求解.
解:(1)则这个长方形的面积是(x+3)2﹣x2=6x+9,
故答案为:6x+9;
(2)5张边长为a的正方形纸片的面积是5a2,
4张边长分别为a、b的矩形纸片的面积是4ab,
3张边长为b的正方形纸片的面积是3b2,
∵4a2+4ab+b2=(2a+b)2,
∴拼成的正方形的边长最长可以为2a+b,
故选:D.
(3)设小正方形的边长为x,大正方形的边长为y,
由图②知,2x+y=m,
由图③知,y﹣2x=n,
∴x=![]() (m﹣n),y=
(m﹣n),y=![]() (m+n),
(m+n),
∴③的大正方形中未被小正方形覆盖部分的面积=(![]() )2﹣4×(
)2﹣4×(![]() )2=mn.
)2=mn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康.在2017年2月周末休息期间,某校九年级一班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计表及统计图,观察并回答下列问题:
类别
雾霾天气的主要成因
百分比
A
工业污染
45%
B
汽车尾气排放
m
C
城中村燃煤问题
15%
D
其他(绿化不足等)
n
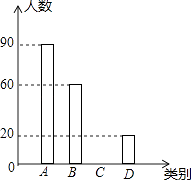
(1)请你求出本次被调查市民的人数及m,n的值,并补全条形统计图;
(2)若该市有800万人口,请你估计持有B,C两类看法的市民共有多少人?
(3)小明同学在四个质地、大小、形状都完全相同的小球上标记A,B,C,D代表四个雾霾天气的主要成因中,放在一个不透明的盒子中,他先随机抽取一个小球,放回去,再随机抽取一个小球,请用画树状图或列表的方法,求出小颖同学刚好抽到B和D的概率.(用A,B,C,D表示各项目) -
科目: 来源: 题型:
查看答案和解析>>【题目】为加快建设经济强、环境美、后劲足、群众富的实力微山,魅力微山,活力微山,幸福微山;聚力脱贫攻坚,全面完成脱贫任务,某乡镇特制定一系列帮扶甲、乙两贫困村的计划,现决定从某地运送1225箱鱼苗到甲、乙两村养殖.若用大、小货车共20辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力和其运往甲、乙两村的运费如表:
车型
载货能力(箱/辆)
运费
甲村(元/辆)
乙村(元/辆)
大货车
70
800
900
小货车
35
400
600
(1)求这20辆车中大、小货车各多少辆?
(2)现安排其中16辆货车前往甲村,其余货车前往乙村,设前往甲村的大货车为x辆,前往甲、乙两村总费用为y元,试求出y与x的函数解析式及x的取值范围;
(3)在(2)的条件下,若运往甲村的鱼苗不少于980箱,请你写出使总费用最少的货车调配方案,并求出最少费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD顶点A,D在⊙O上,边BC经过⊙O上一定P,且PF平分∠AFC,边 AB,CD分别与⊙O相交于点E,F,连接EF.

(1)求证:BC是⊙O的切线;
(2)若FC=2,求PC的长. -
科目: 来源: 题型:
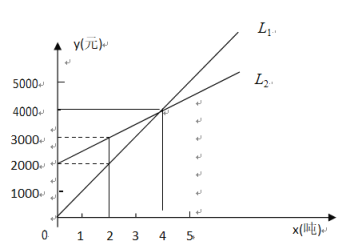
查看答案和解析>>【题目】如图,图象
 反映了某公司产品的销售收入与销售量之间的关系,图象
反映了某公司产品的销售收入与销售量之间的关系,图象 反映了某公司产品的销售成本与销售量之间的关系,则:
反映了某公司产品的销售成本与销售量之间的关系,则:(1)当销售量为2吨时,销售收入为多少元?销售成本呢?此时公司是赢利还是亏损?
(2)当销售量等于多少时该公司收入等于销售成本?
(3)当销售量在什么范围内时,该公司亏损?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,经过原点的抛物线y=ax2+bx+c与x轴的另一个交点为点C;与双曲线y=
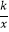 相交于点A,B;直线AB与分别与x轴、y轴交于点D,E.已知点A的坐标为(﹣1,4),点B在第四象限内且到x轴、y轴的距离相等.
相交于点A,B;直线AB与分别与x轴、y轴交于点D,E.已知点A的坐标为(﹣1,4),点B在第四象限内且到x轴、y轴的距离相等.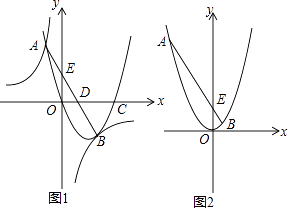
(1)求双曲线和抛物线的解析式;
(2)计算△ABC的面积;
(3)如图2,将抛物线平移至顶点在原点上时,直线AB随之平移,试判断:在y轴的负半轴上是否存在点P,使△PAB的内切圆的圆心在y轴上?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学某学期的四次数学测试成绩(单位:分)如下表:
第一次
第二次
第三次
第四次
甲
87
95
85
93
乙
80
80
90
90
据上表计算,甲、乙两名同学四次数学测试成绩的方差分别为S甲2=17、S乙2=25,下列说法正确的是( )
A.甲同学四次数学测试成绩的平均数是89分
B.甲同学四次数学测试成绩的中位数是90分
C.乙同学四次数学测试成绩的众数是80分
D.乙同学四次数学测试成绩较稳定
相关试题

