【题目】雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康.在2017年2月周末休息期间,某校九年级一班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计表及统计图,观察并回答下列问题:
类别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 | m |
C | 城中村燃煤问题 | 15% |
D | 其他(绿化不足等) | n |
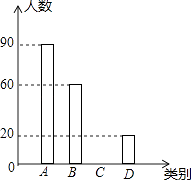
(1)请你求出本次被调查市民的人数及m,n的值,并补全条形统计图;
(2)若该市有800万人口,请你估计持有B,C两类看法的市民共有多少人?
(3)小明同学在四个质地、大小、形状都完全相同的小球上标记A,B,C,D代表四个雾霾天气的主要成因中,放在一个不透明的盒子中,他先随机抽取一个小球,放回去,再随机抽取一个小球,请用画树状图或列表的方法,求出小颖同学刚好抽到B和D的概率.(用A,B,C,D表示各项目)
参考答案:
【答案】
(1)解:本次被调查市民的总人数为:90÷45%=200(人);
m=60÷200=30%,n=20÷200=10%;
C类人数为:200×15%=30(人),
补全条形统计图为:
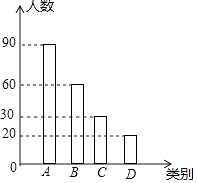
(2)解:800×(30%+15%)=360,
所以估计持有B,C两类看法的市民共有360万人;
(3)解:画树状图为:
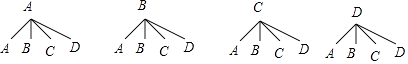
共有16种等可能的结果数,其中小颖同学刚好抽到B和D的结果数为2,
所以小颖同学刚好抽到B和D的概率= ![]() =
= ![]() .
.
【解析】(1)依据总数=频数÷百分比可求得样本总数,然后依据百分比=频数÷总数求得m、n的值,然后计算出C类人数后补全条形统计图;
(2)用800乘以B、C两类人数所占的百分比的和即可;
(3)画树状图展示所有可能的结果数,再找出小颖同学刚好抽到B和D的结果数,最后,再根据概率公式求解即可.
【考点精析】利用统计表和条形统计图对题目进行判断即可得到答案,需要熟知制作统计表的步骤:(1)收集整理数据.(2)确定统计表的格式和栏目数量,根据纸张大小制成表格.(3)填写栏目、各项目名称及数据.(4)计算总计和合计并填入表中,一般总计放在横栏最左格,合计放在竖栏最上格.(5)写好表格名称并标明制表时间;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读第(1)题解答过程填理由,并解答第(2)题
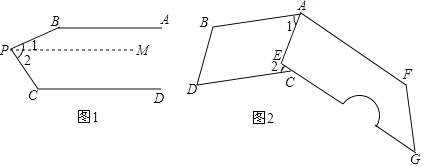
(1)已知:如图1,AB∥CD,P为AB,CD之间一点,求∠B+∠C+∠BPC的大小.
解:过点P作PM∥AB
∵AB∥CD(已知)
∴PM∥CD ,
∴∠B+∠1=180°, .
∴∠C+∠2=180°
∵∠BPC=∠1+∠2
∴∠B+∠C+∠BPC=360°
(2)我们生活中经常接触小刀,如图2小刀刀柄外形是一个直角梯形挖去一个小半圈,其中AF∥EG,∠AEG=90°,刀片上、下是平行的(AB∥CD),转动刀片时会形成∠1和∠2,那么∠1+∠2的大小是否会随刀片的转动面改变,如不改变,求出其大小;如改变,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:(
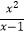 ﹣x﹣1)÷(2﹣
﹣x﹣1)÷(2﹣ 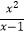 ),其中x2﹣2x﹣3=0.
),其中x2﹣2x﹣3=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AD=5cm,BC=9cm.M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q.
(1)试说明△PCM≌△QDM.
(2)当点P在点B、C之间运动到什么位置时,四边形ABPQ是平行四边形?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为加快建设经济强、环境美、后劲足、群众富的实力微山,魅力微山,活力微山,幸福微山;聚力脱贫攻坚,全面完成脱贫任务,某乡镇特制定一系列帮扶甲、乙两贫困村的计划,现决定从某地运送1225箱鱼苗到甲、乙两村养殖.若用大、小货车共20辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力和其运往甲、乙两村的运费如表:
车型
载货能力(箱/辆)
运费
甲村(元/辆)
乙村(元/辆)
大货车
70
800
900
小货车
35
400
600
(1)求这20辆车中大、小货车各多少辆?
(2)现安排其中16辆货车前往甲村,其余货车前往乙村,设前往甲村的大货车为x辆,前往甲、乙两村总费用为y元,试求出y与x的函数解析式及x的取值范围;
(3)在(2)的条件下,若运往甲村的鱼苗不少于980箱,请你写出使总费用最少的货车调配方案,并求出最少费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD顶点A,D在⊙O上,边BC经过⊙O上一定P,且PF平分∠AFC,边 AB,CD分别与⊙O相交于点E,F,连接EF.

(1)求证:BC是⊙O的切线;
(2)若FC=2,求PC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在乘法公式的学习中,我们采用了构造几何图形的方法研究问题,借助直观、形象的几何模型,加深对乘法公式的认识和理解,从中感悟数形结合的思想方法,感悟几何与代数内在的统一性,根据课堂学习的经验,解决下列问题:
(1)如图①边长为(x+3)的正方形纸片,剪去一个边长为x的正方形之后,剩余部分可拼剪成一个长方形(不重叠无缝隙),则这个长方形的面积为 (用含x的式子表示).
(2)如果你有5张边长为a的正方形纸,4张长、宽分别为a、b(a>b)的长方形纸片,3张边长为b正方形纸片.现从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(不重叠无缝隙),则拼成的正方形的边长最长可以为
A.a+b;B.a+2b;C.a+3b;D.2a+b.
(3)1个大正方形和4个大小完全相同的小正方形按图②③两种方式摆放,求图③中,大正方形中未被4个小正方形覆盖部分的面积.(用含m、n的代数式表示)

相关试题

