【题目】如图1,经过原点的抛物线y=ax2+bx+c与x轴的另一个交点为点C;与双曲线y= ![]() 相交于点A,B;直线AB与分别与x轴、y轴交于点D,E.已知点A的坐标为(﹣1,4),点B在第四象限内且到x轴、y轴的距离相等.
相交于点A,B;直线AB与分别与x轴、y轴交于点D,E.已知点A的坐标为(﹣1,4),点B在第四象限内且到x轴、y轴的距离相等.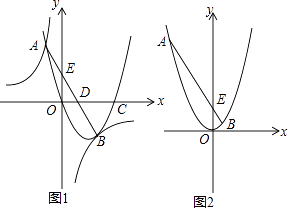
(1)求双曲线和抛物线的解析式;
(2)计算△ABC的面积;
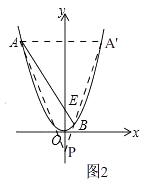
(3)如图2,将抛物线平移至顶点在原点上时,直线AB随之平移,试判断:在y轴的负半轴上是否存在点P,使△PAB的内切圆的圆心在y轴上?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:把点A的坐标代入双曲线的解析式得:k=﹣1×4=﹣4.
所以双曲线的解析式为y=﹣ ![]() .
.
设点B的坐标为(m,﹣m).
∵点B在双曲线上,
∴﹣m2=﹣4,解得m=2或m=﹣2.
∵点B在第四象限,
∴m=2.
∴B(2,﹣2).
将点A、B、C的坐标代入得: 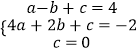 ,
,
解得: 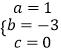 .
.
∴抛物线的解析式为y=x2﹣3x.
(2)解:如图1,连接AC、BC.
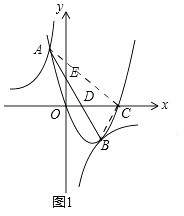
令y=0,则x2﹣3x=0,
∴x=0或x=3,
∴C(3,0),
∵A(﹣1,4),B(2,﹣2),
∴直线AB的解析式为y=﹣2x+2,
∵点D是直线AB与x轴的交点,
∴D(1,0),
∴S△ABC=S△ADC+S△BDC= ![]() ×2×4+
×2×4+ ![]() ×2×2=6;
×2×2=6;
(3)解:存在,理由:如图2,
由原抛物线的解析式为y=x2﹣3x=(x﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∴原抛物线的顶点坐标为( ![]() ,﹣
,﹣ ![]() ),
),
∴抛物线向左平移 ![]() 个单位,再向上平移
个单位,再向上平移 ![]() 个单位,
个单位,
而平移前A(﹣1,4),B(2,﹣2),
∴平移后点A(﹣ ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ),
),
∴点A关于y轴的对称点A'( ![]() ,
, ![]() ),
),
连接A'B并延长交y轴于点P,连接AP,
由对称性知,∠APE=∠BPE,
∴△APB的内切圆的圆心在y轴上,
∵B( ![]() ,
, ![]() ),A'(
),A'( ![]() ,
, ![]() ),
),
∴直线A'B的解析式为y=3x﹣ ![]() ,
,
∴P(0,﹣ ![]() ).
).
【解析】(1)首先将点A的坐标代入反比例函数的解析式求得k的值,然后再求得B的值,最后根据点A的坐标求出双曲线的解析式,进而得出点B的坐标,最后,将点A、B、O三点的坐标代入抛物线的解析式,求得a、b、c的值即可;
(2)由点A和点B的坐标可求得直线AB的解析式,然后将y=0可求得点D的横坐标,最后用三角形的面积和求解即可;
(3)先确定出平移后点A,B的坐标,进而求出点A关于y轴的对称点的坐标,求出直线BA'的解析式即可得出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD顶点A,D在⊙O上,边BC经过⊙O上一定P,且PF平分∠AFC,边 AB,CD分别与⊙O相交于点E,F,连接EF.

(1)求证:BC是⊙O的切线;
(2)若FC=2,求PC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在乘法公式的学习中,我们采用了构造几何图形的方法研究问题,借助直观、形象的几何模型,加深对乘法公式的认识和理解,从中感悟数形结合的思想方法,感悟几何与代数内在的统一性,根据课堂学习的经验,解决下列问题:
(1)如图①边长为(x+3)的正方形纸片,剪去一个边长为x的正方形之后,剩余部分可拼剪成一个长方形(不重叠无缝隙),则这个长方形的面积为 (用含x的式子表示).
(2)如果你有5张边长为a的正方形纸,4张长、宽分别为a、b(a>b)的长方形纸片,3张边长为b正方形纸片.现从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(不重叠无缝隙),则拼成的正方形的边长最长可以为
A.a+b;B.a+2b;C.a+3b;D.2a+b.
(3)1个大正方形和4个大小完全相同的小正方形按图②③两种方式摆放,求图③中,大正方形中未被4个小正方形覆盖部分的面积.(用含m、n的代数式表示)

-
科目: 来源: 题型:
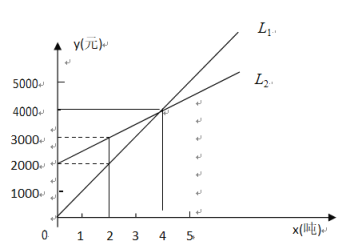
查看答案和解析>>【题目】如图,图象
 反映了某公司产品的销售收入与销售量之间的关系,图象
反映了某公司产品的销售收入与销售量之间的关系,图象 反映了某公司产品的销售成本与销售量之间的关系,则:
反映了某公司产品的销售成本与销售量之间的关系,则:(1)当销售量为2吨时,销售收入为多少元?销售成本呢?此时公司是赢利还是亏损?
(2)当销售量等于多少时该公司收入等于销售成本?
(3)当销售量在什么范围内时,该公司亏损?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学某学期的四次数学测试成绩(单位:分)如下表:
第一次
第二次
第三次
第四次
甲
87
95
85
93
乙
80
80
90
90
据上表计算,甲、乙两名同学四次数学测试成绩的方差分别为S甲2=17、S乙2=25,下列说法正确的是( )
A.甲同学四次数学测试成绩的平均数是89分
B.甲同学四次数学测试成绩的中位数是90分
C.乙同学四次数学测试成绩的众数是80分
D.乙同学四次数学测试成绩较稳定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,BC⊥CD,E是AD的中点,连结BE并延长交CD的延长线于点F.

(1)请连结AF、BD,试判断四边形ABDF是何种特殊四边形,并说明理由.
(2)若AB=4,BC=5,CD=6,求△BCF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

相关试题

