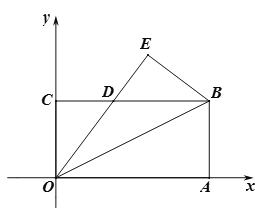
【题目】如图,矩形OABC的边OA,OC分别与坐标轴重合,并且点B的坐标为![]() .将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.
.将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.
(1)求证:△OBD为等腰三角形;
(2)求点E的坐标;
(3)坐标平面内是否存在一点F,使得以点B,E,F,O为顶点的四边形是平行四边形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)证明见解析;(2)点E的坐标为![]() ;(3)F点坐标为
;(3)F点坐标为![]() ,
,![]() ,
,![]() .
.
【解析】
(1)根据折叠的性质,得到△OBE≌△OBA,由此得到∠EOB=∠AOB,然后根据矩形的性质和平行线的性质得到OD=BD,即△OBD是等腰三角形;
(2)过点E作![]() 轴于F交BC于G,设CD的长为
轴于F交BC于G,设CD的长为![]() ,则
,则![]() ,由(1)值OD=8-x,然后根据勾股定理求出CD、OB、BD的长,再根据AAS证得△OCD≌△BED,得到
,由(1)值OD=8-x,然后根据勾股定理求出CD、OB、BD的长,再根据AAS证得△OCD≌△BED,得到![]() ,最后根据三角形的面积求出EG的长,进而利用矩形的性质和勾股定理求出E点的坐标;
,最后根据三角形的面积求出EG的长,进而利用矩形的性质和勾股定理求出E点的坐标;
(3)根据平行四边形的判定与性质,分类讨论F点的坐标即可.
(1)∵![]() 是由
是由![]() 折叠所得
折叠所得
∴![]() ≌
≌![]() .,
.,
∴![]() ,
,
又∵四边形OABC是矩形
∴![]() .,
.,
∴![]()
∴![]() ,
,
∴![]() 为等腰三角形;
为等腰三角形;
(2)过点E作![]() 轴于F交BC于G
轴于F交BC于G
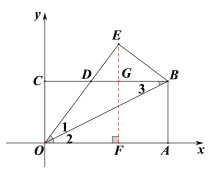
设CD的长为![]() ,则
,则![]()
由(1)知![]()
∵四边形OABC是矩形
∴![]()
∴在![]() 中
中![]()
即![]()
解得![]()
即![]()
由(1)知![]() ≌
≌![]()
∴![]()
∴![]()
∴ 在△OCD和△BED中
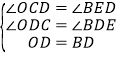
∴△OCD≌△BED
∴![]()
∵![]() 轴
轴
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
即![]()
∴![]() .
.
∴在![]() 中
中![]()
∵![]()
∴四边形OFGC是矩形
∴![]()
![]() .
.
∴点E的坐标为![]() ;
;
(3)![]()
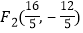
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四个命题:
①对应角和面积都相等的两个三角形全等;
②“若x2﹣x=0,则x=0”的逆命题;
③若关于x、y的方程组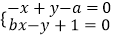 有无数多组解,则a=b=1;
有无数多组解,则a=b=1;
④将多项式5xy+3y﹣2x2y因式分解,其结果为﹣y(2x+1)(x﹣3).
其中正确的命题的序号为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)计算:( )﹣2+|
)﹣2+| 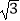 ﹣2|+3tan30°
﹣2|+3tan30°
(2)先化简,再求值: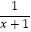 ﹣
﹣ 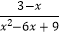 ÷
÷ 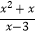 ,其中x=﹣
,其中x=﹣  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C( , ),B→C( , ),C→ (+1, );
(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-2),请在图中标出P的位置;

(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(4)若图中另有两个格点M、N,且M→A(3-a,b-4),M→N(5-a,b-2),则N→A应记为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”
译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”
设井深为x尺,根据题意列方程,正确的是( )

A. 3(x+4)=4(x+1) B. 3x+4=4x+1
C. 3(x﹣4)=4(x﹣1) D.
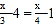
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
6
a
b
x
-2
1
…
(1)可求得x=______,第2016个格子中的数为______;
(2)判断:前m个格子中所填整数之和是否可能为2016?若能,求出m的值,若不可能,请说明理由;
(3)如果x,y为前3格子中的任意两个数,那么所有的|x-y|的和可以通过计算|6-a|+|a-6|+|a-b|+|b-a|+|6-b|+|b-6|得到.若x,y为前20格子中的任意两个数,则所有的|a-b|的和为______.
-
科目: 来源: 题型:
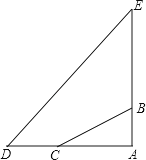
查看答案和解析>>【题目】在一次综合实践活动中,小明要测某地一座古塔AE的高度.如图,已知塔基顶端B(和A、E共线)与地面C处固定的绳索的长BC为80m.她先测得∠BCA=35°,然后从C点沿AC方向走30m到达D点,又测得塔顶E的仰角为50°,求塔高AE.(人的高度忽略不计,结果用含非特殊角的三角函数表示)
相关试题

