【题目】我们定义:在一个图形上画一条直线,若这条直线既平分该图形的面积,又平分该图形的周长,我们称这条直线为这个图形的“等分积周线”.
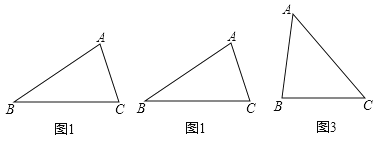
(1)如图1,在△ABC中,AB=BC,且BC≠AC,请你在图1中用尺规作图作出△ABC的一条“等分积周线”;
(2)在图1中,过点C能否画出一条“等分积周线”?若能,说出确定的方法;若不能,请说明理由.
(3)如图3,在△ABC中,AB=BC=6cm,AC=8cm,请你不过△ABC的顶点,画出△ABC的一条“等分积周线”,并说明理由.
参考答案:
【答案】(1)作图见解析;
(2)不能,理由见解析;
(3)作图见解析,理由见解析.
【解析】(1)作线段AC的中垂线BD即可得出答案;(2)若直线CD平分△ABC的面积,那么S△ADC=S△DBC,得出AC≠BC,进而得出答案;(3)在AC上取一点F,使得FC=AB=6,在BC上取一点E,使得BE=2,作直线EF,则EF是△ABC的等分积周线,结合全等三角形的判定与性质得出答案.
解:
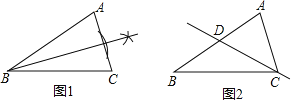
(1)如图1所示:作线段AC的中垂线BD或∠B的平分线即可;
(2)不能,理由:如图2,若直线CD平分△ABC的面积,那么S△ADC=S△DBC,
∴AD=BD,
∵AC≠BC,
∴AD+AC≠BD+BC,
∴过点C不能画出一条“等分积周线”
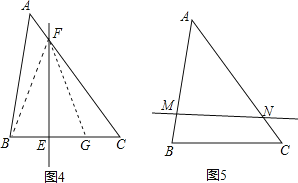
(3)如图4,在AC上取一点F,使得FC=AB=6,在BC上取一点E,使得BE=2,
作直线EF,则EF是△ABC的等分积周线,
理由:由作图可得:AF=AC-FC=8-6=2,在CB上取一点G,使得CG=AF=2,则有AB+AF=CF+CG,
∵AB=BC,
∴∠A=∠C,
在△ABF和△CFG中
∴△ABF≌△CFG(SAS),
∴S△ABF=S△CFG,
又易得BE=EG=2,
∴S△BFE=S△EFG,
∴S△EFC=S四边形ABEF,
AF+AB+BE=CE+CF=10,
∴EF是△ABC的等分积周线,
若如图5,当BM=2cm,AN=6cm时,直线MN也是△ABC的等分积周线.(其实是同一条),
另外本问的说理也可以通过作高,进行相关计算说明).
“点睛”此题主要考查了应用与设计作图和全等三角形的判定与性质和勾股定理等知识,根据题意正确分割图形是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:3x(x-2)=4-2x. (2)用配方法解方程:
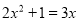
-
科目: 来源: 题型:
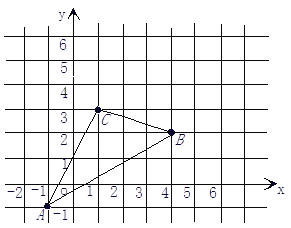
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标。
(2)若把△ABC向上平移3个单位,再向右平移2个单位得△A'B'C',在 图 中 画 出 △ABC变化位置,并 写 出 A'、B'、C'的坐标。
(3)求出S△ABC
-
科目: 来源: 题型:
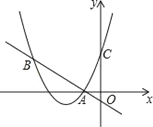
查看答案和解析>>【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.
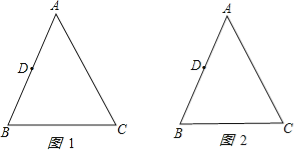
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形具有稳定性的是( )
A.正方形
B.矩形
C.平行四边形
D.直角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】若正多边形的一个内角是160°,则该正多边形的边数是__________.
相关试题

