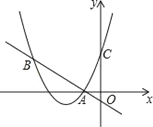
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.
参考答案:
【答案】(1)抛物线解析式为y=x2+4x+3,一次函数解析式为y=﹣x﹣1;(2)由图象可知,满足(x+2)2+m≥kx+b的x的取值范围为x﹣4或x≥﹣1.
【解析】(1)先利用待定系数法先求出m,再求出点B坐标,利用方程组求出太阳还是解析式.
(2)根据二次函数的图象在一次函数的图象上面即可写出自变量x的取值范围.
解:(1)∵抛物线y=(x+2)2+m经过点A(﹣1,0),∴0=1+m,∴m=﹣1,∴抛物线解析式为y=(x+2)2﹣1=x2+4x+3,∴点C坐标(0,3),∵对称轴x=﹣2,B、C关于对称轴对称,∴点B坐标(﹣4,3),∵y=kx+b经过点A、B,
∴![]() ,解得
,解得![]() ,
,
∴一次函数解析式为y=﹣x﹣1,
(2)由图象可知,写出满足(x+2)2+m≥kx+b的x的取值范围为x<﹣4或x>﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解关于x的一元二次方程x2﹣2x﹣3=0,配方后的方程可以是( )
A. (x﹣1)2=4 B. (x+1)2=4 C. (x﹣1)2=16 D. (x+1)2=16
-
科目: 来源: 题型:
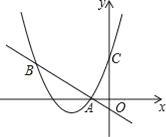
查看答案和解析>>【题目】(1)解方程:3x(x-2)=4-2x. (2)用配方法解方程:
-
科目: 来源: 题型:
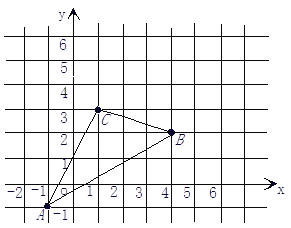
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标。
(2)若把△ABC向上平移3个单位,再向右平移2个单位得△A'B'C',在 图 中 画 出 △ABC变化位置,并 写 出 A'、B'、C'的坐标。
(3)求出S△ABC
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:在一个图形上画一条直线,若这条直线既平分该图形的面积,又平分该图形的周长,我们称这条直线为这个图形的“等分积周线”.
(1)如图1,在△ABC中,AB=BC,且BC≠AC,请你在图1中用尺规作图作出△ABC的一条“等分积周线”;
(2)在图1中,过点C能否画出一条“等分积周线”?若能,说出确定的方法;若不能,请说明理由.
(3)如图3,在△ABC中,AB=BC=6cm,AC=8cm,请你不过△ABC的顶点,画出△ABC的一条“等分积周线”,并说明理由.
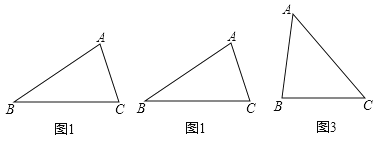
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.
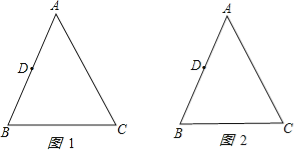
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形具有稳定性的是( )
A.正方形
B.矩形
C.平行四边形
D.直角三角形
相关试题

