【题目】若∠A与∠B的两边分别垂直,请判断这两个角的数量关系.
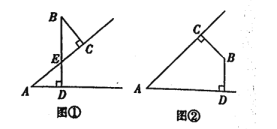
(1)如图①,∠A与∠B的数量关系是____,如图②,∠A与∠B的数量关系是____.
(2)请从图①或图②中选择一种情况说明理由。
参考答案:
【答案】(1)∠A=∠B(相等) ,∠A+∠B=180°(互补);(2)见解析.
【解析】
1)如果一个角的两边与另一个角的两边分别垂直,那么这两个角的关系是相等或互补;
(2)根据垂直的量相等的角都等于90°,对顶角相等,即可得出∠A=∠B,同样根据垂直的定义以及四边形的内角和等于360°,即可得出∠A+∠B=360°-90°-90°=180°.
(1)如图①,∠A=∠B(相等);如图②,∠A+∠B=180°(互补);
故答案为:相等,互补;
(2)选题图①,∵BC⊥AC,BD⊥AD,
∴∠ECB=∠ADE=90°.
又∵∠A=180°-∠EDA-∠AED,∠B=180°-∠BCE-∠BEC,∠AED=∠BEC,
∴∠A=∠B.
选题图②,∵BC⊥AC,BD⊥AD,
∴∠ECB=∠ADE=90°.
∵四边形的内角和等于360°,
∴∠A+∠B=360°-90°-90°=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重合的四边形EFGH,EH=12cm,EF=l6cm则边AD的长是( )
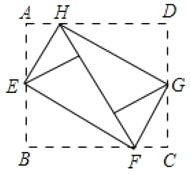
A.12cmB.16cmC.20cmD.24cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P.已知
 ,
,  ,
, ,
, .
.(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC平分∠BAD, ∠ACD=∠ABC=90°,E、F分别为AC、CD的中点,∠D=62°,则∠BEF的度数为_______.

-
科目: 来源: 题型:
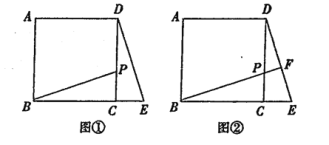
查看答案和解析>>【题目】探究:如图①,在正方形ABCD中,点P在边CD上(不与点C、D重合),连结BP.将△BCP绕点C顺时针旋转至△DCE,点B的对应点是点D,旋转的角度是 度.
应用:将图①中的BP延长交边DE于点F,其它条件不变,如图②.求∠BFE的度数.
拓展:如图②,若DP=2CP,BC=3,则四边形ABED的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”,这批单车分为A、B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动,投放A、B两种款型的单车共100辆,总价值36800元.求本次试点投放的A型车、B型车的辆数.
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A、B两车型的数量比进行投放,且投资总价值不低于184万元.问整个城区全面铺开时投放的A型车、B型车至少多少辆?
相关试题

