【题目】如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P.已知![]() ,
, ![]() ,
,![]() ,
,![]() .
.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.

参考答案:
【答案】(1)66°;(2)15.5.
【解析】
(1)根据全等三角形的性质得到∠ABC=∠DBE,计算即可;
(2)根据全等三角形的性质求出BE、DE,根据三角形的周长公式计算即可.
(1)∵△ABC≌△DBE,
∴∠ABC=∠DBE.
∴∠ABC-∠DBC =∠DBE-∠DBC,即∠ABD=∠CBE.
∵∠ABD+∠DBC+∠CBE =∠ABE,
∴∠CBE=![]() (∠ABE-∠DBC)=
(∠ABE-∠DBC)=![]() ×(162°-30°)=66°.
×(162°-30°)=66°.
(2)∵△ABC≌△DBE,
∴DE=AC=AD+DC=5,BE=BC=4,
∴△CDP与△BEP的周长和=DC+DP+PC+BP+PE+BE=DC+DE+BC+BE=2.5+5+4+4=15.5.
-
科目: 来源: 题型:
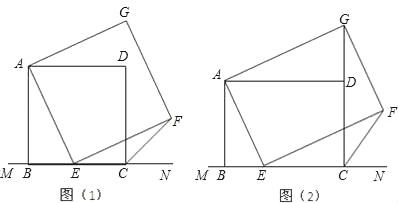
查看答案和解析>>【题目】如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重合的四边形EFGH,EH=12cm,EF=l6cm则边AD的长是( )
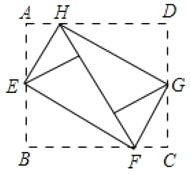
A.12cmB.16cmC.20cmD.24cm
-
科目: 来源: 题型:
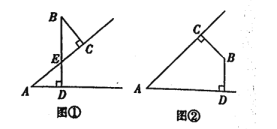
查看答案和解析>>【题目】若∠A与∠B的两边分别垂直,请判断这两个角的数量关系.
(1)如图①,∠A与∠B的数量关系是____,如图②,∠A与∠B的数量关系是____.
(2)请从图①或图②中选择一种情况说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC平分∠BAD, ∠ACD=∠ABC=90°,E、F分别为AC、CD的中点,∠D=62°,则∠BEF的度数为_______.

-
科目: 来源: 题型:
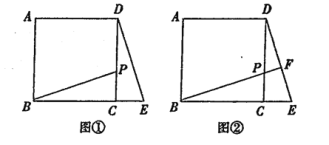
查看答案和解析>>【题目】探究:如图①,在正方形ABCD中,点P在边CD上(不与点C、D重合),连结BP.将△BCP绕点C顺时针旋转至△DCE,点B的对应点是点D,旋转的角度是 度.
应用:将图①中的BP延长交边DE于点F,其它条件不变,如图②.求∠BFE的度数.
拓展:如图②,若DP=2CP,BC=3,则四边形ABED的面积是 .
相关试题

