【题目】如图,一种拉杆式旅行箱的示意图,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,(点A、B、C在同一条直线上),在箱体的底端装有一圆形滚轮⊙A,其直径为10cm,⊙A与水平地面切于点D,过A作AE∥DM.当人的手自然下垂拉旅行箱时,人感觉较为舒服,已知某人的手自然下垂在点C处且拉杆达到最大延伸距离时,点C距离水平地面(40 ![]() +5)cm,求此时拉杆箱与水平面AE所成角∠CAE的大小及点B到水平地面的距离.
+5)cm,求此时拉杆箱与水平面AE所成角∠CAE的大小及点B到水平地面的距离. 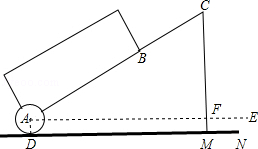
参考答案:
【答案】解:CF=40 ![]() +5﹣5=40
+5﹣5=40 ![]() (m). 则sin∠CAF=
(m). 则sin∠CAF= ![]() =
= ![]() ,
,
则∠CAF=60°,
如图,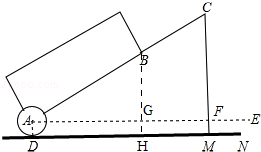
作BH⊥AF于点G,交DM于点H.
则BG∥CF,
∴△ABG∽△ACF.![]() ,
,
即 ![]() ,
,
解得:BG=25 ![]() ,
,
点B到水地面的距离为(25 ![]() +5 )cm
+5 )cm
【解析】先用三角函数求出∠CAF,再用相似三角形得出比例式求出BG,即可.
【考点精析】本题主要考查了切线的性质定理和相似三角形的应用的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,
收费标准如下:
人数m
0<m≤100
100<m≤200
m>200
收费标准(元/人)
90
85
75
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费10 800元,若两校联合组团只需花赞18 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗? 为什么?
(2)两所学校报名参加旅游的学生各有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
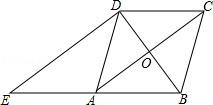
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划从一厂家购进若干部新型手机以满足市场需求.已知该厂家生产三种不同型号的手机,出厂价分别是甲种型号手机1800元/部,乙种型号手机600元/部,丙种型号手机1200元/部.商场在经销中,甲种型号手机可赚200元/部,乙种型号手机可赚100元/部,丙种型号手机可赚120元/部.
(1)若商场用6万元同时购进两种不同型号的手机共40部,并恰好将钱用完,请你通过计算分析进货方案;
(2)在(1)的条件下,求盈利最多的进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号里(将各数用逗号分开):﹣4,0.62,
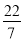 ,18,0,﹣8.91,+100
,18,0,﹣8.91,+100正数:{______…};负数:{______…};整数:{______…};分数:{______…}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据图示的对话解答下列问题.

求:(1)a,b的值;
(2)8﹣a+b﹣c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学老师布置了一道思考题“计算:(-
 )÷(
)÷(
 )”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
)”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.小明的解法:原式的倒数为(

 )÷(
)÷( )=(
)=(
 )×(-12)=-4+10=6,所以(-
)×(-12)=-4+10=6,所以(- )÷(
)÷(
 )=
)= .
.(1)请你判断小明的解答是否正确,并说明理由.
(2)请你运用小明的解法解答下面的问题.
计算:(-
 )÷(
)÷(
 +
+ ).
).
相关试题

