【题目】(题文)如图,在平面直角坐标系中,矩形OABC的顶点A(6,0),C(0,2![]() ),过y轴上的点D(0,3
),过y轴上的点D(0,3![]() ),作射线DM与x轴平行,点P,Q分别是射线DM与x轴正半轴上的动点,满足∠PQO=60°.设点P的横坐标为x(0≤x≤9),△OPQ与矩形的重叠部分的面积为y,则能大致反映y与x函数关系的图象是( )
),作射线DM与x轴平行,点P,Q分别是射线DM与x轴正半轴上的动点,满足∠PQO=60°.设点P的横坐标为x(0≤x≤9),△OPQ与矩形的重叠部分的面积为y,则能大致反映y与x函数关系的图象是( )

A.  B.
B.  C.
C.  D.
D. 
参考答案:
【答案】C
【解析】
根据选项时间,探究临界点前后的图形变化,分类讨论.分别采用相似三角形知识表示相应线段即可.
由已知当t=3时,点Q与点A重合,
由题意OD=3![]() ,∠PQO=60°,
,∠PQO=60°,

当0≤t≤3时,
∵DM与x轴平行,
∴△PEF∽△POQ,
∴![]() ,
,
∴EF=![]() ,
,
∴y=![]() (EF+OQ)CO=
(EF+OQ)CO=![]() ,
,
则选项A、D排除,
当t=5时,PQ过点B,当t=9时,点P过点B,
∴当5≤t≤9时,如图,
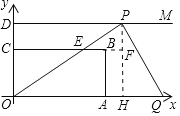
过点P作PH⊥OQ于点H,延长CB交PH于点F,
由已知,HQ=3,
则OH=x-3,
∵CB∥OQ,
∴△PEF∽△POH,
∴EF=![]() x,
x,
∴EB=![]() x(x6)=
x(x6)=![]() x+6,
x+6,
∴y=![]() (EB+OA)AB=
(EB+OA)AB=![]() (
(![]() x+6+6)2
x+6+6)2![]() =
= ![]() x+12
x+12![]() ,
,
此时y是x的一次函数,
∴选项D排除,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, 垂直平分
垂直平分 ,分别交
,分别交 、
、 于点
于点 、
、 ,
, 垂直平分
垂直平分 ,分别交
,分别交 ,
, 于点
于点 、
、 .
.⑴如图①,若
 ,求
,求 的度数;
的度数;⑵如图②,若
 ,求
,求 的度数;
的度数;⑶若

 ,直接写出用
,直接写出用 表示
表示 大小的代数式.
大小的代数式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程|x2﹣x|﹣a=0,给出下列四个结论:①存在实数a,使得方程恰有2个不同的实根; ②存在实数a,使得方程恰有3个不同的实根;③存在实数a,使得方程恰有4个不同的实根;④存在实数a,使得方程恰有6个不同的实根;其中正确的结论个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系中.
(1)作出△ABC关于
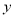 轴对称的
轴对称的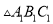 ,并写出
,并写出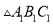 三个顶点的坐标:
三个顶点的坐标: 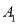 ( ),
( ),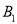 ( ),
( ),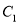 ( );
( );(2)直接写出△ABC的面积为 ;
(3)在
 轴上画点P,使PA+PC最小.
轴上画点P,使PA+PC最小.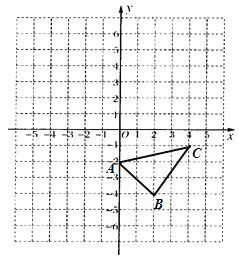
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,AB=6cm,AC=8cm,以斜边BC上距离B点6cm的点P为中心,把这个三角形按逆时针方向旋转90°至△DEF,则旋转前后两个三角形重叠部分的面积是_______cm2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与x轴交于点C,与y轴交于点B,点A(1,3),点B(0,2).连接AO
(1)求直线AB的解析式;
(2)求三角形AOC的面积.

相关试题

