【题目】如图,在Rt△ABC中,∠A=90°,AB=6cm,AC=8cm,以斜边BC上距离B点6cm的点P为中心,把这个三角形按逆时针方向旋转90°至△DEF,则旋转前后两个三角形重叠部分的面积是_______cm2.

参考答案:
【答案】![]()
【解析】
过P作PM⊥AC于M,PN⊥DF于N,由以斜边BC上距离B点6cm的点P为中心,把这个三角形按逆时针方向旋转90°至△DEF,根据旋转的性质得∠KPH=90°,∠KGH=90°,得∠MPN=90°,易证Rt△PCM≌Rt△PFN,得到PM=PN,则四边形PMGN为正方形,Rt△PNK≌Rt△PMH,由PM∥AB,PM:AB=CP:CB,得到PM=![]() ,于是S重叠=S正方形PMGN=(
,于是S重叠=S正方形PMGN=(![]() )2=
)2=![]() .
.
过P作PM⊥AC于M,PN⊥DF于N,如图,

∵以斜边BC上距离B点6cm的点P为中心,把这个三角形按逆时针方向旋转90°至△DEF,
∴∠KPH=90°,∠KGH=90°,
∴∠MPN=90°,
∴∠KPN=∠MPH,
∵PC=PF,∠C=∠F,
∴Rt△PCM≌Rt△PFN,
∴PM=PN,
∴四边形PMGN为正方形,Rt△PNK≌Rt△PMH,
∴S重叠部分=S正方形PMGN,
∵∠A=90°,AB=6,AC=8,
∴BC=10,
而PB=6,则PC=4,
又∵PM∥AB,
∴PM:AB=CP:CB,
∴PM=![]() ,
,
∴S重叠=S正方形PMGN=(![]() )2=
)2=![]() (cm2).
(cm2).
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程|x2﹣x|﹣a=0,给出下列四个结论:①存在实数a,使得方程恰有2个不同的实根; ②存在实数a,使得方程恰有3个不同的实根;③存在实数a,使得方程恰有4个不同的实根;④存在实数a,使得方程恰有6个不同的实根;其中正确的结论个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图,在平面直角坐标系中,矩形OABC的顶点A(6,0),C(0,2
 ),过y轴上的点D(0,3
),过y轴上的点D(0,3 ),作射线DM与x轴平行,点P,Q分别是射线DM与x轴正半轴上的动点,满足∠PQO=60°.设点P的横坐标为x(0≤x≤9),△OPQ与矩形的重叠部分的面积为y,则能大致反映y与x函数关系的图象是( )
),作射线DM与x轴平行,点P,Q分别是射线DM与x轴正半轴上的动点,满足∠PQO=60°.设点P的横坐标为x(0≤x≤9),△OPQ与矩形的重叠部分的面积为y,则能大致反映y与x函数关系的图象是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系中.
(1)作出△ABC关于
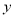 轴对称的
轴对称的 ,并写出
,并写出 三个顶点的坐标:
三个顶点的坐标:  ( ),
( ), ( ),
( ), ( );
( );(2)直接写出△ABC的面积为 ;
(3)在
 轴上画点P,使PA+PC最小.
轴上画点P,使PA+PC最小.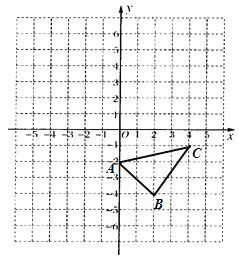
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与x轴交于点C,与y轴交于点B,点A(1,3),点B(0,2).连接AO
(1)求直线AB的解析式;
(2)求三角形AOC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程:
 =
= =
=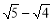 =
= -2;
-2; =
= =
= .
.请回答下列问题:
(1)观察上面的解题过程,请直接写出式子
 = ;
= ;(2)观察上面的解题过程,请直接写出式子
 = ;
= ;(3)利用上面所提供的解法,请求
 +···+
+···+ 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

相关试题

