搜索
【题目】如图，一座钢结构桥梁的框架是△ABC，水平横梁BC长18米，中柱AD高6米，其中D是BC的中点，且AD⊥BC．
（1）求sinB的值；
（2）现需要加装支架DE、EF，其中点E在AB上，BE＝2AE，且EF⊥BC，垂足为点F，求支架DE的长．
参考答案：
【答案】（1）sinB＝
；（2）DE＝5．
【解析】试题分析：（1）在Rt△ABD中，利用勾股定理求出AB，再根据sinB=
计算即可；
（2）由EF∥AD，BE=2AE，可得
,求出EF、DF即可利用勾股定理解决问题；
试题解析：（1）在Rt△ABD中，∵BD=DC=9，AD=6，
∴AB=
=
=3
，∴sinB==
=
．
（2）∵EF∥AD，BE=2AE，∴，∴
，∴EF=4，BF=6，
∴DF=3，在Rt△DEF中，DE=
=
=5．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c．
（Ⅰ）若抛物线的顶点为A（﹣2，﹣4），抛物线经过点B（﹣4，0）
①求该抛物线的解析式；
②连接AB，把AB所在直线沿y轴向上平移，使它经过原点O，得到直线l，点P是直线l上一动点．
设以点A，B，O，P为顶点的四边形的面积为S，点P的横坐标为x，当4+6
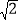≤S≤6+8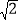时，求x的取值范围；（Ⅱ）若a＞0，c＞1，当x=c时，y=0，当0＜x＜c时，y＞0，试比较ac与l的大小，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】 我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释，例如：图A可以用来解释
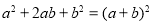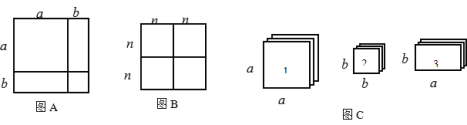
，实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.（1）图B可以解释的代数恒等式是 ；
（2）现有足够多的正方形和矩形卡片，如图C：
①若要拼出一个面积为（3a+b）（a+2b）的矩形，则需要1号卡片 张，2号卡片 张，3号卡片 张；
②试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形，使该矩形的面积为6a2+7ab+2b2，并利用你画的图形面积对6a2+7ab+2b2进行因式分解.
-
科目： 来源： 题型：
查看答案和解析>>【题目】规定：sin（﹣x）=﹣sinx，cos（﹣x）=cosx，sin（x+y）=sinxcosy+cosxsiny．
据此判断下列等式成立的是 （写出所有正确的序号）
①cos（﹣60°）=﹣
；②sin75°=
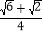；③sin2x=2sinxcosx；
④sin（x﹣y）=sinxcosy﹣cosxsiny．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，BC=a ，AB=c，AC=b，则不能作为判定△ABC是直角三角形的条件的是（ ）
A.
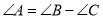B.∠A∶∠B∶∠C=1∶4∶3C.a∶b∶c =7∶24∶25D.a∶b∶c =4∶5∶6
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，点D在边BC上，连接AD .
（1）试利用尺规作图，求作：线段AE，使得AE是线段AD绕点A沿逆时针方向旋转得到的，且
（保留作图痕迹，不写作法于证明过程）；（2）连接DE交AC于F，若
，求
的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，从地面上的点A看一山坡上的电线杆PQ，测得杆顶端点P的仰角是45°，向前走6m到达B点，测得杆顶端点P和杆底端点Q的仰角分别是60°和30°．
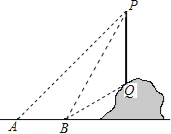
（1）求∠BPQ的度数；
（2）求该电线杆PQ的高度（结果精确到1m）．
备用数据：
，
．
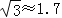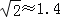相关试题
