【题目】在△ABC中,AB=AC,BC=12,E为边AC的中点,
(1)如图1,过点E作EH⊥BC,垂足为点H,求线段CH的长;
(2)作线段BE的垂直平分线分别交边BC、BE、AB于点D、O、F.
①如图2,当∠BAC=90°时,求BD的长;
②如图3,设tan∠ACB=x,BD=y,求y与x之间的函数表达式和tan∠ACB的最大值.

参考答案:
【答案】(1)3(2)5(3)①![]() ②
②![]()
【解析】试题分析:(1)点A作AG⊥BC交BC于点G,则EH∥AG,由等腰三角形的性质得CG=6,再由E为AC中点可得H为CG的中点.
(2)①过点E作![]() 于点H,设
于点H,设![]() ,在Rt△EDH中可得
,在Rt△EDH中可得![]() ,解方程求出x的值;由
,解方程求出x的值;由![]()
![]() ,可得
,可得![]() ,
, ![]() ,在
,在![]() 中,根据勾股定理列出关系式
中,根据勾股定理列出关系式![]() ,然后整理可得y与x之间的函数表达式;求tan∠ACB的最大值有两种方法一是利用正切的增减性,二是利用数形结合.
,然后整理可得y与x之间的函数表达式;求tan∠ACB的最大值有两种方法一是利用正切的增减性,二是利用数形结合.
解:(1)点A作AG⊥BC交BC于点G.

∵![]() ,
,
∴![]() ,
,
∵E为AC中点,EH∥AG,
∴H为CG的中点,∴CH=3,
⑵①过点E作![]() 于点H,
于点H,

∵△ABC是等腰直角三角形,则CH=EH=3,
设![]() ,则
,则![]() ,
, ![]() ,
,
Rt△EDH中, ![]() ,
,
解之得, ![]() ,
,
即BD=5,
②∵![]()
![]() ,
,
∴![]() ,
, ![]() ,
,
在![]() 中,
中,
![]() ,
,
∴![]() ,
,
方法一:由![]() 得,
得, ![]() ,
,
当y有最大值时,x有最大值.即tan∠ACB有最大值.
∴当y=12时, ![]() ,
, ![]() (负的舍去),
(负的舍去),
∴tan∠ACB最大值为![]() ,
,
或方法二:当点D与点C重合时,tan∠ACB最大,
![]() ,
,
![]() .
.
BC边的高为![]() ,
,
此时tan∠ACB=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空完成推理过程:
如图,∠1=∠2,∠A=∠D, 求证:∠B=∠C.
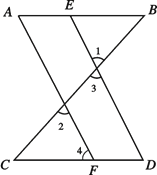
证明:∵∠1=∠2(已知),
∠1=∠3( ),
∴∠2=∠3(等量代换).
∴AF∥________( ).
∴∠D=∠4(两直线平行,同位角相等 ).
∵∠A=∠D(已知),
∴∠A=∠4(等量代换).
∴AB∥CD(内错角相等,两直线平行).
∴∠B=∠C( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选
取该校100名学生进行调查,要求每名学生只选出一类自己最喜爱的节目,根据调查结果 绘制了不完整的条形图和扇形统计图(如图),
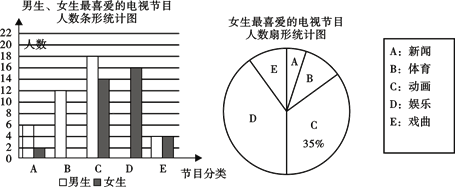
根据图中提供的信息,解答下列问题:
(1)这次抽样调查的女生人数是_______人;
(2)扇形统计图中, “A”组对应的圆心角度数为_______,并将条形图中补充完整;
(3)若该校有 1800 名学生,试估计全校最喜欢新闻和戏曲的学生一共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长青农产品加工厂与 A,B 两地有公路、铁路相连.这家工厂从 A 地购买一批原料甲运回工厂,经过加工后制成产品乙运到 B 地,其中原料甲和产品乙的重量都是正整数.
已知铁路运价为 2 元/(吨·千米),公路运价为 8 元/(吨·千米).

(1)若由 A 到 B 的两次运输中,原料甲比产品乙多 9 吨,工厂计划支出铁路运费超 过 5700 元,公路运费不超过 9680 元.问购买原料甲有哪几种方案,分别是多少吨?
(2)由于国家出台惠农政策,对运输农产品的车辆免收高速通行费,并给予一定的 财政补贴,综合惠农政策后公路运输价格下降 m( 0 m 4 且 m 为整数)元, 若由 A 到 B 的两次运输中,铁路运费为 5760 元,公路运费为 5100 元,求 m 的 值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依此规律,则点A2017的坐标是( )
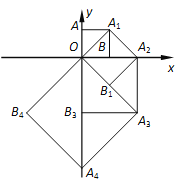
A. (0,21008) B. (21008,21008) C. (21009,0) D. (21009,-21009)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D为边AB上一点,CD绕点D顺时针旋转90°至DE,CE交AB于点G.已知AD=8,BG=6,点F是AE的中点,连接DF,求线段DF的长___.
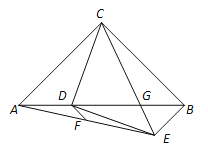
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋中有3个分别标有数字-1、1、2的小球,它们除标的数字不同外无其他区别.
(1)随机地从口袋中取出一小球,求取出的小球上标的数字为负数的概率;
(2)随机地从口袋中取出一小球,放回后再取出第二个小球,求两次取出的数字的和等于0的概率.
相关试题

