【题目】如图,图①中△ABC是等边三角形,其边长是3,图②中△DEF是等腰直角三角形,∠F=90°,DF=EF=3.
(1)若S1为△ABC的面积,S2为△DEF的面积,S3=![]() AB·BC·sinB,S4=
AB·BC·sinB,S4=![]() DE·DF·sinD,请通过计算说明S1与S3,S2与S4之间有着怎样的关系;
DE·DF·sinD,请通过计算说明S1与S3,S2与S4之间有着怎样的关系;
![]()
(2)在图③中,∠P=α(α为锐角),OP=m,PQ=n,△OPQ的面积为S,请你根据第(1)小题的解答,直接写出S与m,n以及α之间的关系式,并给出证明.
参考答案:
【答案】(1) S1=S3,S2=S4 (2) S=![]() mnsinα.
mnsinα.
【解析】(1)图①,过点A作AH⊥BC于点H,由已知先求出AH的长,再利用三角形面积公式进行计算可得S1;图②直接利用三角形面积公式进行求解可得S2;
根据已知数据可计算得出S3,计算S4时,先利用勾股定理求出DE的长,再代入式子进行计算即可,根据以上数据进行比较即可得;
(2)根据(1)中的发现直接写出然后进行证明即可得.证明思路:过点O作OM⊥PQ,垂足为点M,在Rt△OPM中,先求出OM长,再利用三角形面积公式进行计算即可得证.
(1)如图,过点A作AH⊥BC于点H,
∵△ABC是等边三角形,AH⊥BC,∴AH=AB·sinB=3sin60°=3×![]() =
=![]() ,
,
∴S1=![]() ×3×
×3×![]() =
=![]() ,
,
∵△DEF是等腰直角三角形,∠F=90°,DF=EF=3,
∴∠D=45°,S2=![]() =
=![]() ,
,
S3=![]() AB·BC·sinB=
AB·BC·sinB=![]() ×3×3×sin60°=
×3×3×sin60°=![]() ,
,
在Rt△DEF中,由勾股定理得DE=![]() =3
=3![]() ,
,
∴S4=![]() DE·DF·sinD=
DE·DF·sinD=![]() ×3
×3![]() ×3×
×3×![]() =
=![]() ,
,
∴S1=S3,S2=S4;
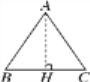
(2)S=![]() mnsinα,证明如下:
mnsinα,证明如下:
如图,过点O作OM⊥PQ,垂足为点M,
在Rt△OPM中,∠OMP=90°,∴OM=OP·sinP,
∵∠P=α,OP=m,∴OM=msinα,
∴S=![]() PQ·OM=
PQ·OM=![]() mnsinα.
mnsinα.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,一次函数y=
 x+3的图像与y轴交于点A,点M在正比例函数y=
x+3的图像与y轴交于点A,点M在正比例函数y=  x的图像x>0的那部分上,且MO=MA(O为坐标原点).
x的图像x>0的那部分上,且MO=MA(O为坐标原点).
(1)求线段AM的长;
(2)若反比例函数y=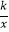 的图像经过点M关于y轴的对称点M′,求反比例函数解析式,并直接写出当x>0时,
的图像经过点M关于y轴的对称点M′,求反比例函数解析式,并直接写出当x>0时,  x+3与
x+3与 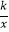 的大小关系.
的大小关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划投入一笔资金采购一批紧俏商品,经过市场调查发现,如果月初出售,可获利15﹪,并可用本金和利润再投资其他商品,到月末又可获利10﹪;如果月末出售可获利30﹪,但要付出仓储费用700元.
(1)若商场投资
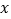 元,分别用含
元,分别用含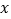 的代数式表示月初出售和月末出售所获得的利润;
的代数式表示月初出售和月末出售所获得的利润;(2)若商场投资40000元,问选择哪种销售方式获利较多?此时获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家超市以相同的价格出售同样的商品,但为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超过400元后,超过部分按原价七折优惠;在乙超市购买商品只按原价的八折优惠;设顾客累计购物
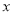 元(
元(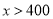 )
)(1)用含
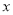 的代数式分别表示顾客在两家超市购买所付的费用。
的代数式分别表示顾客在两家超市购买所付的费用。(2)当
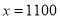 时,试比较顾客到哪家超市购物更加优惠。
时,试比较顾客到哪家超市购物更加优惠。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.

(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面选项中符合代数式书写要求的是 ( )
A.
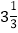 y2 B. ay·3 C.
y2 B. ay·3 C. 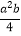 D. a×b+c
D. a×b+c -
科目: 来源: 题型:
查看答案和解析>>【题目】为控制禽流感病毒传播,某地关闭活禽交易市场,冷冻鸡肉销量上升,某公司在春节期间采购冷冻鸡肉60箱销往城市和乡镇,已知冷冻鸡肉在城市销售平均每箱的利润y1(百元)与销售数量x(箱)的关系为y1=
 在乡镇销售平均每箱的利润y2(百元)与销售数量t(箱)的关系为y2=
在乡镇销售平均每箱的利润y2(百元)与销售数量t(箱)的关系为y2=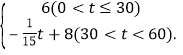
(1)t与x的关系是 ,将y2转换为x为自变量的函数,则y2= ;
(2)设春节期间售完全部冷冻鸡肉可获得总利润W(百元),当在城市销售量x(箱)的范围是0<x≤20时,求W与x的关系式(总利润=在城市销售利润+在乡镇销售利润);
(3)经测算,在20<x≤30的范围内,可以获得最大总利润,求这个最大总利润,并求出此时x的值.
相关试题

